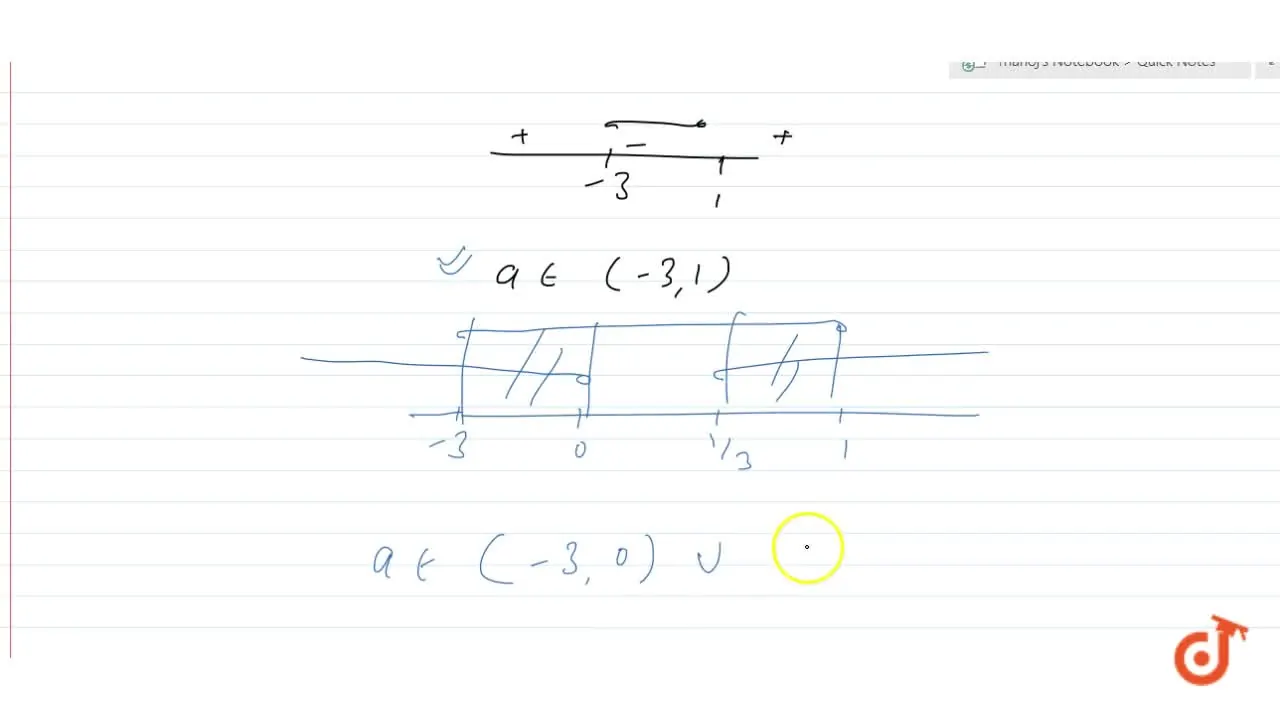
If the point (a2,a+1) lies in the angle between the lines 3x−y+1=0 and x+2y−5=0 containing the origin, then find the value of a.
Step by step video & image solution for If the point (a^2,a+1) lies in the angle between the lines 3x-y+1=0 and x+2y-5=0 containing the origin, then find the value of adot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Find the angle between the lines x−2y+5=0 and x+3y−5=0.
View SolutionFind the angle between the lines x−2y+3=0and3x+y−1=0.
View SolutionFind the angle between the lines 3x=5and3x+5y−2=0
View SolutionThe point (a2,a+1) lies in the angle between the lines 3x+y+1=0 and x+2y−5=0 containing the origin. If a is an integer, then the sum of all possible values of a is
View SolutionFind the angle between the lines 3x=5and3x+5y−2=0.
View SolutionFind the angle between two lines x+2y−111=0 and x−3y−19=0
View SolutionThe angle between the lines 3x−y+5=0,x+3y−2=0 is
View SolutionFind the angle between the lines x+3y−8=0and2x−3y+6=0.
View SolutionThe point P(a2,a+1) lis in the angle between the two given lines,
3x−y+1=0,x+2y−5=0 containing the origin. Find the number of integral values of a.View SolutionIf the point (2cosθ,2sinθ), for θ∈(0,2π) lines in the region between the lines x+y=2andx−y=2 containing the origin, then θ lies in
View Solution