Two sides of a rhombus are along the lines,x−y+1=0 and 7x−y−5=0 . If its diagonals intersect at (−1,−2) , then which one of the following is a vertex of this rhombus ? (1) (−3,−9) (2) (−3,−8) (3) (13,−83) (4) (−103,−73)

A

(-3, -8)

B

(13,−83)

C

((−103,−73)

D

(-3, -9)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

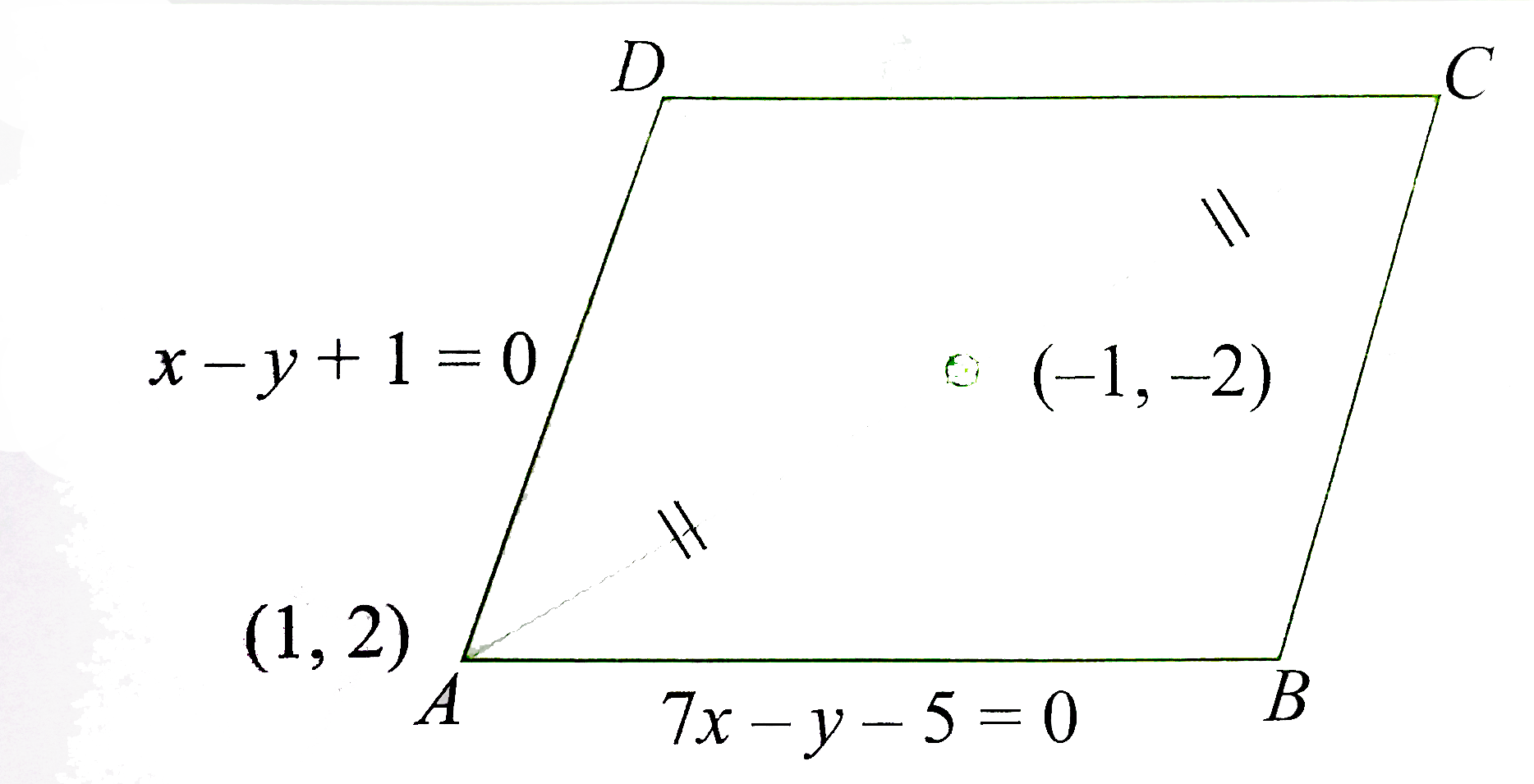
ocr_image
On solving equation of AB and AD, vertex A(1, 2)
∵(−1,−2) is midpoint of AC, vertex C is (−3,−6).
Line BC is parallel to AD passing through point C, hence its equation is x-y-3 =0
Line DC is parallel to AB passing through ponit C, hence its equation is 7x-y+15=0
Hence other vertices are
B(13,−83) and D(−73,−43)

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Two sides of a parallelogram are along the lines x+y=3 and x=y+3. If its diagonals intersect at (2, 4) , then one of its vertices is

    A(2, 6)
    B(2,1)
    C(3, 5)
    D(6,3)

  • The sides of a rhombus ABCD are parallel to the lines x−y+2=0 and 7x−y+3=0, If the diagonals of the rhombus intersect at P(1,2) and the vertex A (different from the origin) is on the y-axis then the ordinate of A is:

    A2
    B52
    C74
    D72

  • One side of a rectangle lies along the line 4x + 7y + 5 = 0. Two of its vertices are (-3, 1) and (1, 1). Which of the following is not an equation of the other three straight lines?

    A14x - 8y = 6
    B7x - 4y = -25
    C4 x + 7y = 11
    D14 -8y = - 25