The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is
A
2+√2
B
2−√2
C
1+√2
D
1−√2
Video Solution
Text Solution
The correct Answer is:B
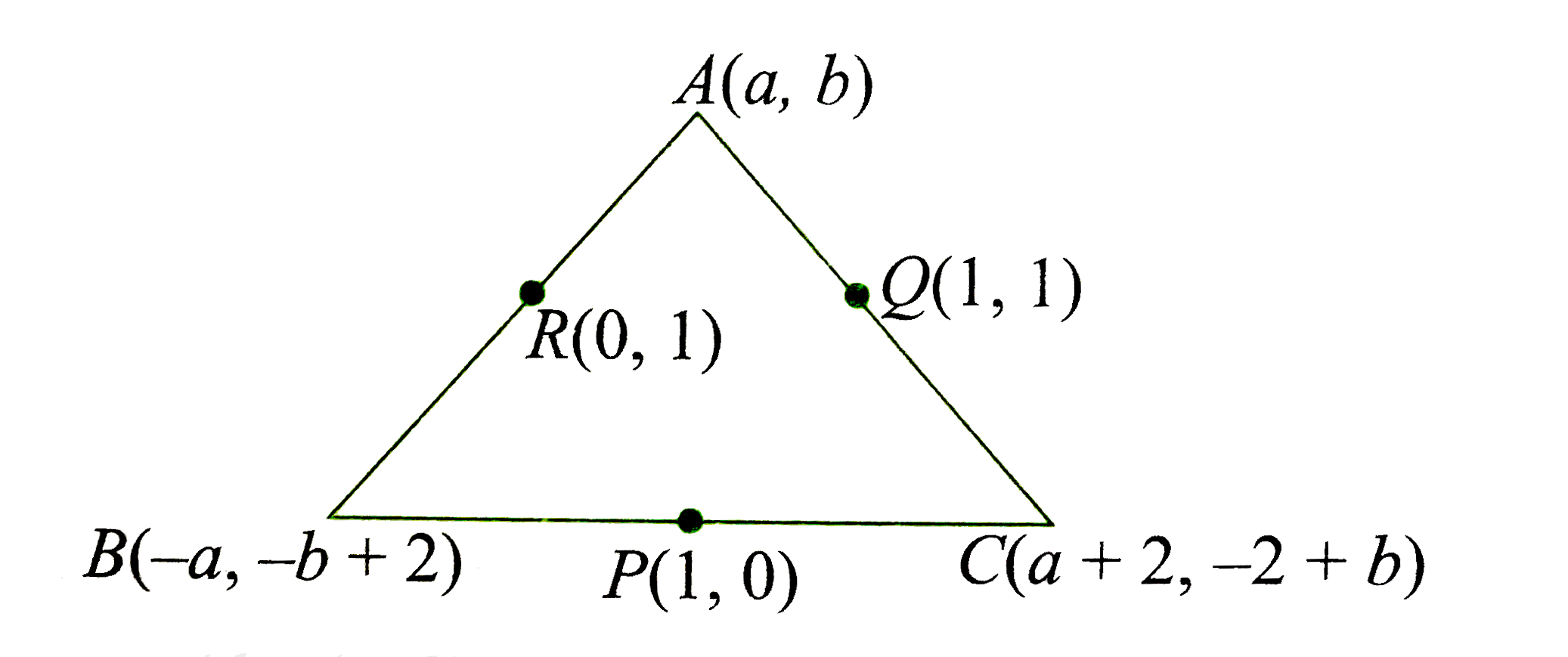
Let vertex A be (a, b).
R is mid point of AB.
∴B is (−a,−b+2)
Pis mid point of BC.
∴C is (a+2,−2+b)
Q is mid point of AC.
∴a=0 and b=2
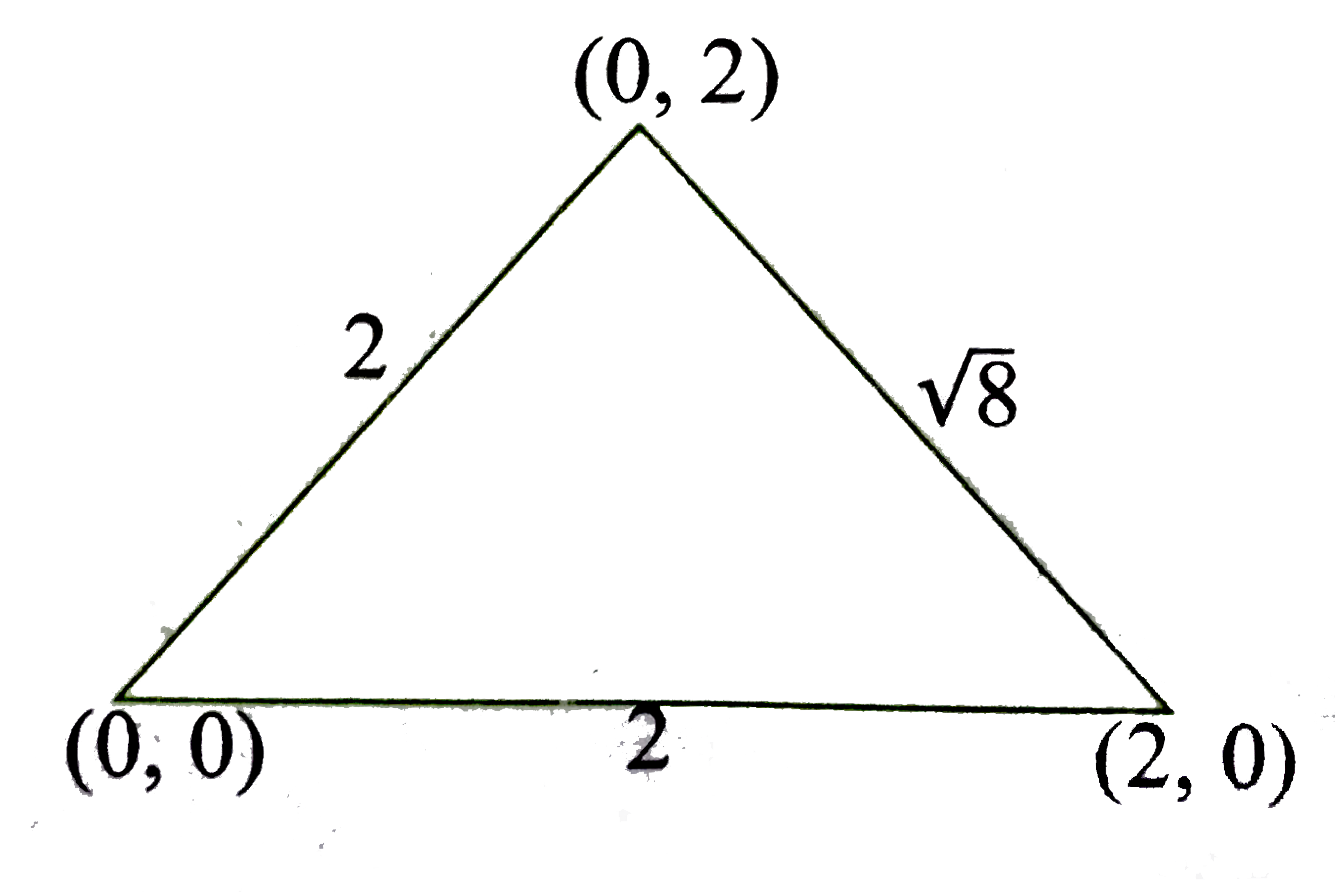
∴ Abscissa of in center
Ix=0×2+0×√8+2×22+2+2√2
∴Ix=44+2√2
⇒Ix=22+√2×2−√22−√2
⇒Ix=2(2−√2)2=2−√2
|
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:JEE Advanced Previous Year
Explore 4 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Numerical)
Explore 13 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Knowledge Check
The x-coordinates of the incentre of the triangle that has the coordinates of mid-point of its sides as (0, 1), (1, 1) and (1, 0), is
A2+√2B2−√2C1+√2D1−√2The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is
A2+√2B2−√2C1+√2D1−√2The x -coordinate of the incentre of the triangle that has the coordinates of mid-points its sides are (0,1), (1,1) and (1, 0) is
A2+√2B2−√2C1+√2D1−√2
Find the inradius of a Δ whose vertices (0,0) (0,3) and (4,0)
View SolutionThe incentre of the triangle formed by the line 3x+4y−12=0 with the coordinate axis is
View SolutionFind the centroid of the triangle mid points of whose sides are (1,2,−3),(3,0,1)and(−1,1,4)
View SolutionThe coordinates of incentre of a triangle with A(0,3) and B(4,0) and origin as vertices are
View SolutionThe coordinates of the orthocenter of the triangle that has the coordinates of midpoint of its sides as ( 0,0) , ( 1,2) and ( - 6,3) is
View Solution

