Question

The equation of an altitude of an equilateral triangle is $\sqrt{3}x+y=2\sqrt{3}$ and one of its vertices is $(3,\sqrt{3})$ then the possible number of triangles is

Options

A. 1
B. 2
C. 3
D. 4

Answer

B

Explanation

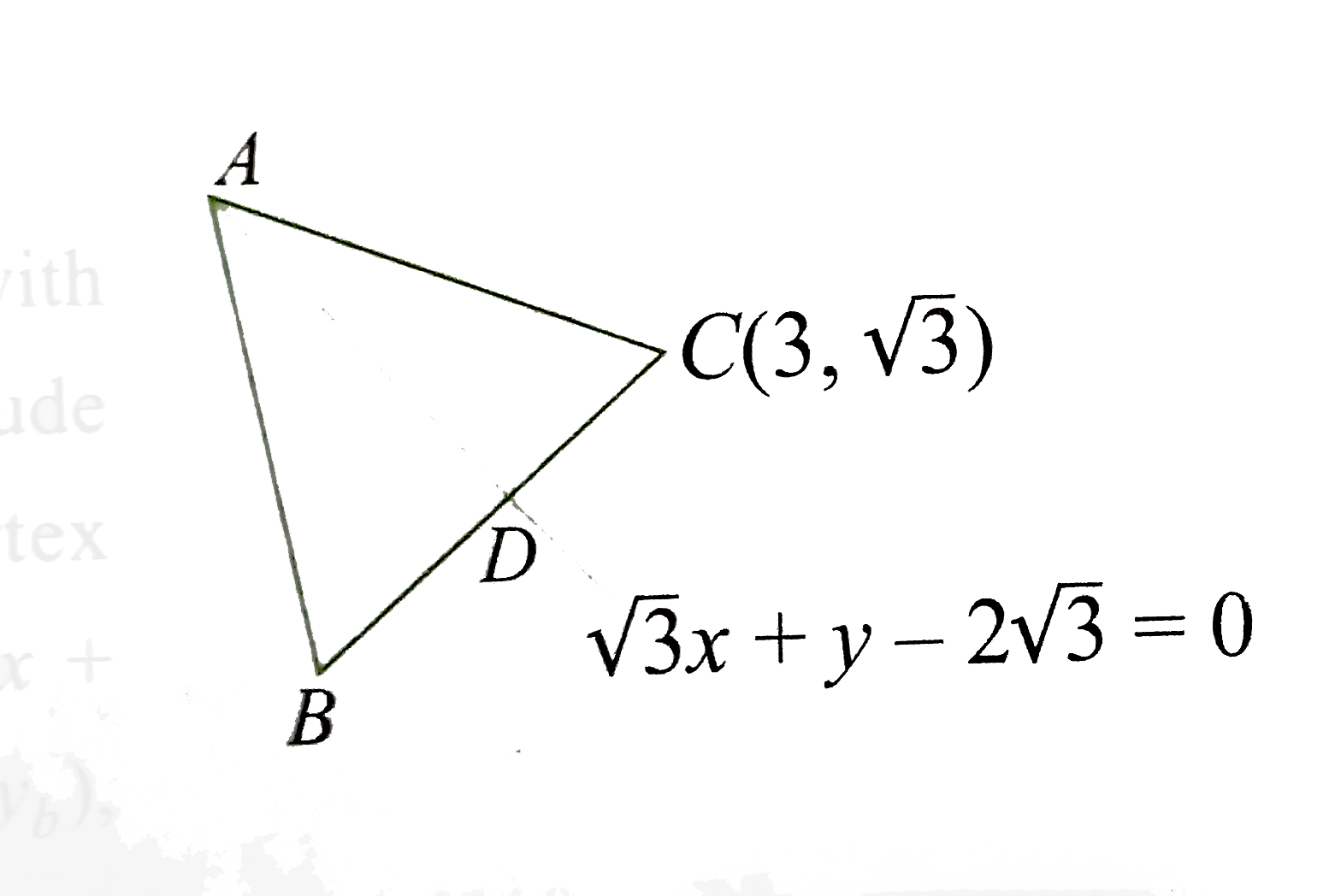
Let the triangle be ABC with `C-=(3, sqrt(3))` and the altitude drawn through the vertex (meeting BC at D) be `sqrt(3)x + y-2sqrt(3) = 0. "If " B is (x_(b), y_(b))`,
then we have
`(x_(b)-3)/(sqrt(3)) = (y_(b)-sqrt(3))/(1) = (2(3sqrt(3) + sqrt(3)-2sqrt(3)))/(4) = -sqrt(3)`
`"or " x_(b) = 0, y_(b) = 0`
and the coordinates of D are `(3//2, sqrt(3)//2).` Let the coordinates of vertex A be `(x_(a), y_(a)).` Then,
`(x_(a) -(3//2))/(-1//2) = (y_(a) - (sqrt(3)//2))/(sqrt(3)//2) = +-3`
`or (x_(a), y_(a))-=(0, 2sqrt(3)) " or "(3, -sqrt(3))`
Hence, the remaining vertices are (0,0) and `(0, 2sqrt(3))` or (0,0) and `(3, -sqrt(3))`. Also, the orthocenter is `(1, sqrt(3)) " or " (2,0)`.