Two sides of a triangle are parallel to the coordinate axes. If the slopes of the medians through the acute angles of the triangle are 2 and m, the m= 12 (b) 2 (c) 4 (d) 8
1/2
2
4
8
The correct Answer is:A, D
m1=Slope of AD=−a2b
m2=Slope of BE=−2ab
∴m1m2=14
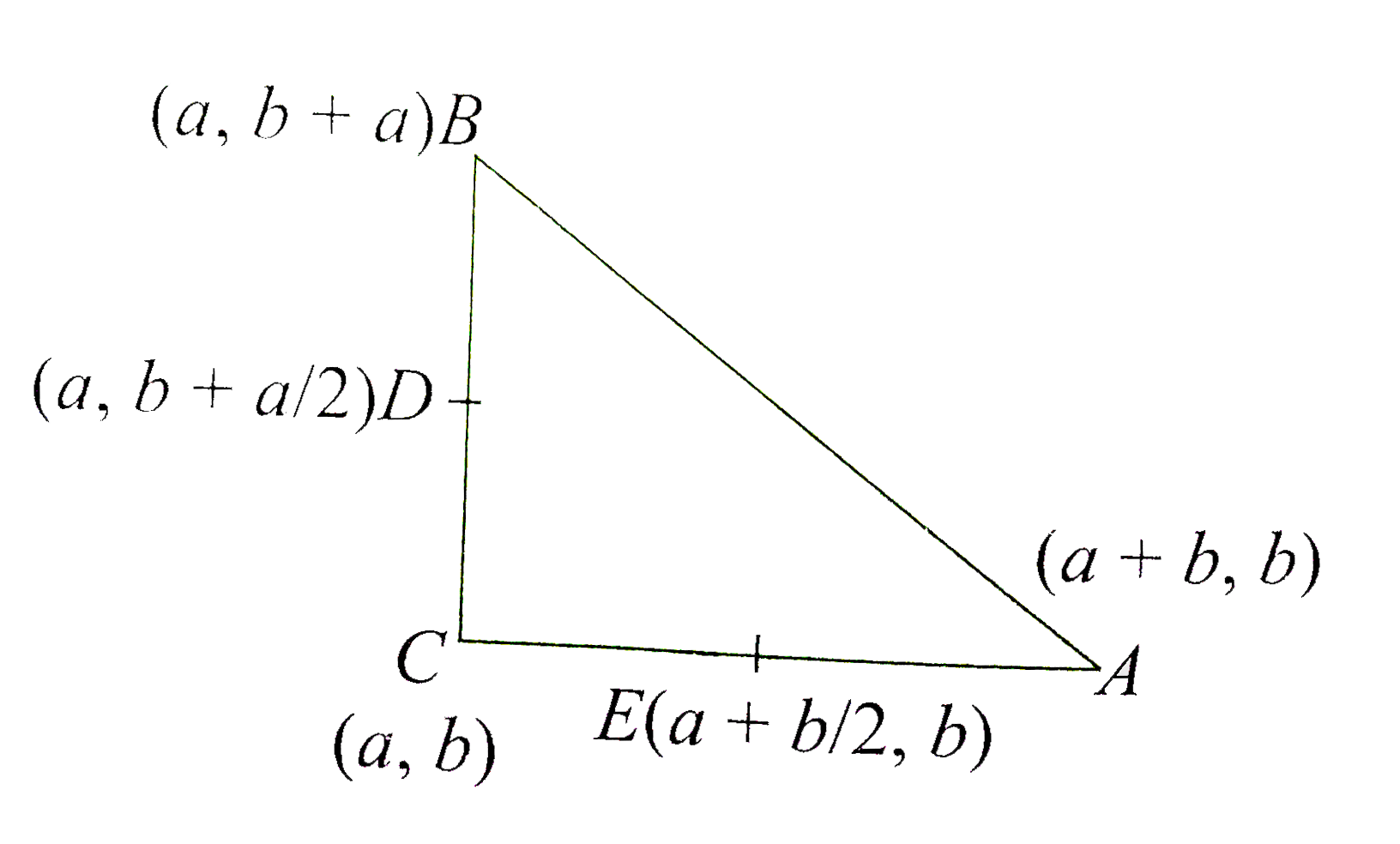
If m1=2, then m2=m=8
If m2=2,then m1=m=1/2.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Matrix)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Single)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
The lengths of the medians through acute angles of a right-angled triangle are 3 and 4. Find the area of the triangle.
View SolutionTwo sides of a triangle are along the coordinate axes and the medians through the vertices (other than the origin) are mutually perpendicular. The number of such triangles is/are zero (b) two (c) four (d) infinite
View Solution
Knowledge Check
The vertices of a triangle are A (3,-2), B (-2, 1) and C (5,2). Then the length of the median through B is
A√67 unitsB√37 unitsC√35 unitsD6 unitsIf a plane meets the coordinate axes at A,B and C such that the centroid of the triangle is (1,2,4) then the equation of the plane is
Ax+2y+4z=12B4x+2y+z=12Cx+2y+4z=3D4x+2y+z=3If a plane meets the coordinate axes at A, B and C such that the centroid of the triangle is (1,2,4),then the equation of the plane is
Ax+2y+4z=12B4x+2y+z=12Cx+2y+4z=3D4x+2y+z=3
The sides of a triangle are m, n and √m2+n2+mn., What is the sum of the acute angles of the triangle?
View SolutionIt is desired to construct a right angled triangle ABC (∠C=π2) in x-y plane so that its sides are parallel to coordinates axis and the medians through A and B lie on the lines y=3x+1 and y=mx+2 respectively. The values of m for which such a triangle is possible is/are
View SolutionIf a2+b2+c2=ab+bc+ca where a, b, c are the sides of a triangle, then the largest angle of that triangle is
View SolutionA triangle must have (1) Exactly two acute angles (2) At least two acute angles (3) Exactly three acute angles (4) At most one acute angle
View SolutionIf two sides of an obtuse angled triangle are 8 cm and 15 cm and third sides is x, then
View Solution

