$θ_{1} and θ_{2}$ are the inclination of lines $L_{1} and L_{2}$ with the x-axis. If $L_{1} and L_{2}$ pass through $P (x, y)$ , then the equation of one of the angle bisector of these lines is

$\frac{x - x_{1}}{cos (\frac{θ_{1} + θ_{2}}{2})} = \frac{y - y_{1}}{sin (\frac{θ_{1} + θ_{2}}{2})}$

$\frac{x - x_{1}}{-sin (\frac{θ_{1} - θ_{2}}{2})} = \frac{y - y_{1}}{cos (\frac{θ_{1} - θ_{2}}{2})}$

$\frac{x - x_{1}}{sin (\frac{θ_{1} + θ_{2}}{2})} = \frac{y - y_{1}}{cos (\frac{θ_{1} + θ_{2}}{2})}$

$\frac{x - x_{1}}{-sin (\frac{θ_{1} + θ_{2}}{2})} = \frac{y - y_{1}}{cos (\frac{θ_{1} + θ_{2}}{2})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

Updated on:21/07/2023

The area of triangle formed by the lines $l_{1} and l_{2}$ and the x-axis is:

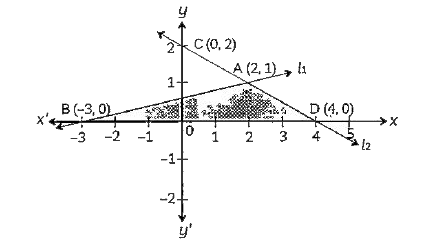A7 sq. units
B $\frac{9}{2}$ sq.units
C $\frac{7}{2}$ sq.units
D4 sq. units
A line L passeds through the points $(1, 1) and (2, 0)$ and another line L' passes through $(\frac{1}{2}, 0)$ and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
A $\frac{15}{8}$
B $\frac{25}{4}$
C $\frac{25}{8}$
D $\frac{25}{16}$
Let $L_{1} and L_{2}$ be the foollowing straight lines.
$L_{1} : \frac{x - 1}{1} = \frac{y}{- 1} = \frac{z - 1}{3} and L_{2} : \frac{x - 1}{- 3} = \frac{y}{- 1} = \frac{z - 1}{1}$
Suppose the striight line $L : \frac{x - α}{l} = \frac{y - m}{m} = \frac{z - γ}{- 2}$ lies in the plane containing $L_{1} and L_{2}$ and passes throug the point of intersection of $L_{1} and L_{2}$ if the L bisects the acute angle between the lines $L_{1} and L_{2}$ , then which of the following statements is /are TRUE ?
A $α - γ = 3$
B $l + m = 2$
C $α - γ = 1$
D $l + m = 0$