Two sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are $y = \frac{x}{\sqrt{3}}, y = \sqrt{3} x$ Then possible coordinates of B is / are ('O' being the origin)

A

$(1 + \sqrt{3}, 1 + \sqrt{3})$

B

$(- 1 - \sqrt{3}, - 1 - \sqrt{3})$

C

$(3 + \sqrt{3}, 3 + \sqrt{3})$

D

$(\sqrt{3} - 1, \sqrt{3} - 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

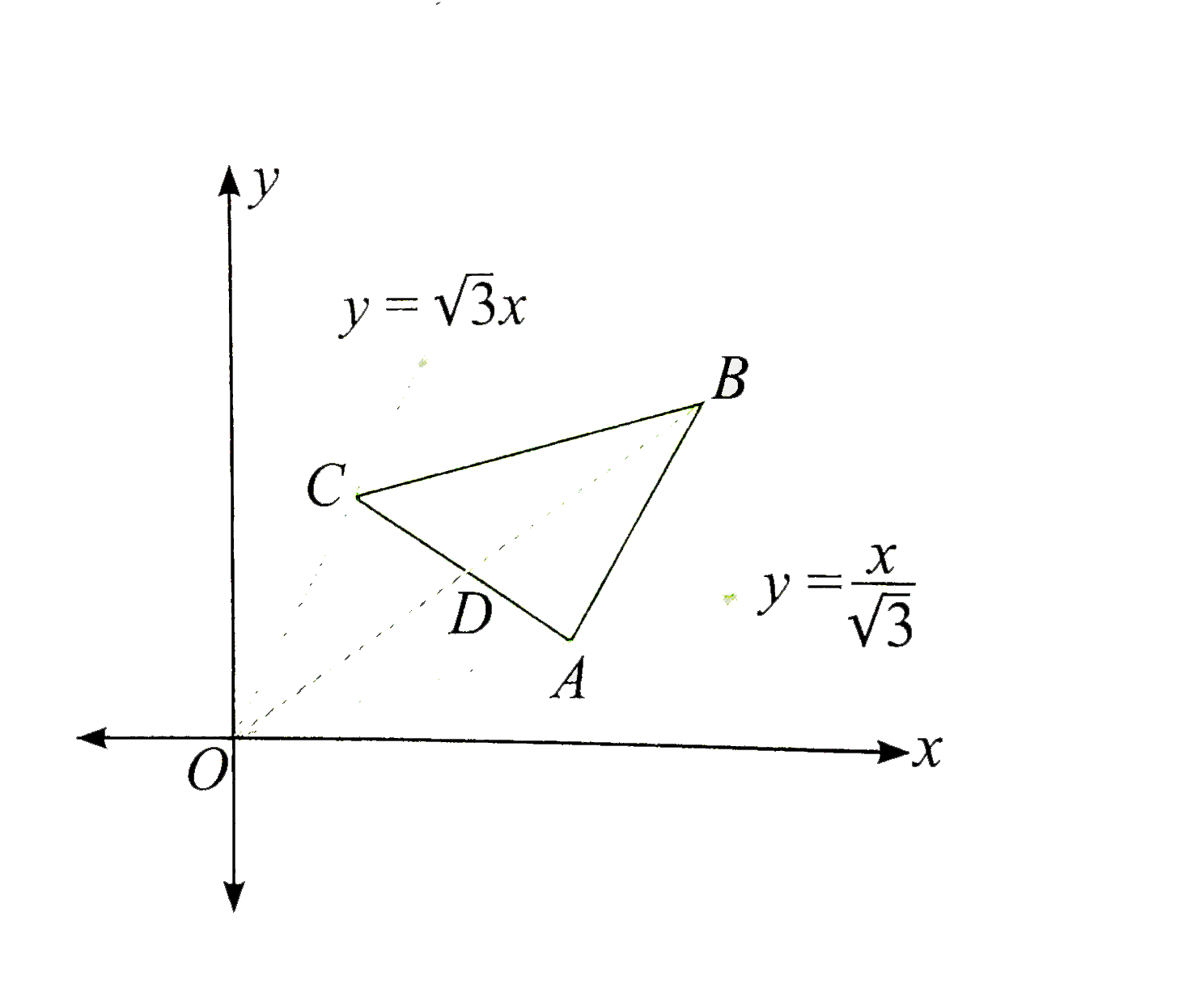
$Here, ∠ C O A = 30^{\circ} .$
Area of rhombus $= 2 \times \frac{1}{2} \times O A \times O C sin 30^{\circ}$
$or 2 = \frac{1}{2} x^{2}$
or OA = OC =2
$Also, ∠ O A B = 150^{\circ}$
$∴ cos 150^{\circ} = \frac{O A^{2} + A B^{2} - O B^{2}}{2 O A \times A B}$
$O B^{2} = 8 + 4 \sqrt{3} or O B = \sqrt{2} (\sqrt{3} + 1)$
Hence, the coordinates of B are $(\pm \sqrt{2} (\sqrt{3} + 1) cos 45^{\circ}, \pm \sqrt{2} (\sqrt{3} + 1) sin 45^{\circ}) .$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two sides of a rhombus OABC (O being origin) lying entirely in first or third quadrant of area 2 sq. units are $y = \frac{1}{\sqrt{3}} x$ and $y = \sqrt{3} x$ . Then possible co ordinates of B are
A $(1 + \sqrt{3}, 1 + \sqrt{3})$
B $(- 1 - \sqrt{3}, - 1 - \sqrt{3})$
C $(\sqrt{3} - 1, \sqrt{3} - 1)$
Dnone
Question 2 - Select One
The area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the line $x = \sqrt{3} y$ is :
A $\frac{π}{3}$
B $\frac{π}{2}$
C $π$
D $\frac{π}{5}$
Question 3 - Select One
Find the area lying in the first quadrant and bounded by the curve $y = x^{3}$ and the line $y = 4 x .$
A2
B3
C4
D5

CENGAGE-STRAIGHT LINES-Exercise (Multiple)

Home
Ask Doubt
Profile