At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.
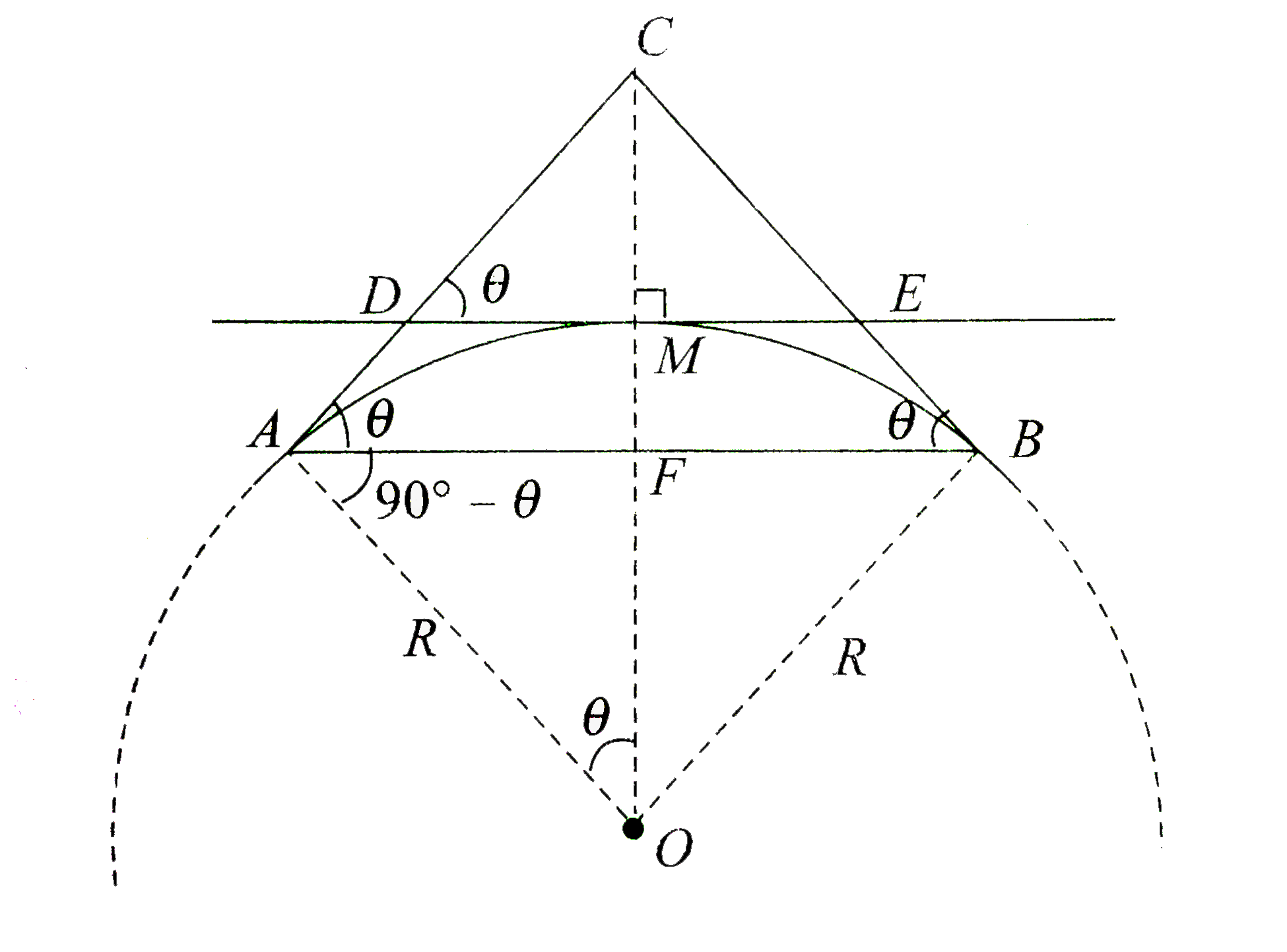
Let Δ1=Area of triangle ABC
and Δ2=Area of triangle CDE
In AFO,AF=Rsinθ and OF=Rcosθ
MF=OM−OF=R−Rcosθ
In triangle OAC,OC=Rsecθ
∴ CM=OC−OM=Rsecθ−R
∴ CF=CM+MF=Rsecθ−Rcosθ
So, Δ1=12AB.CF
=122Rsinθ.R(secθ−cosθ)
=R2tanθ(1−cos2θ)
In triangle CMD,DM=CMcotθ
=(Rsecθ=−R)cotθ
∴ Δ2=122(Rsecθ−R)cotθ.(Rsecθ−R)
=R2(1−cos2θ)2cos2θ.tanθ
∴ Δ1Δ2=tanθ(1−cos2θ)cos2θtanθ(1−cosθ)2
=sin2θ(1+cosθ)(1−cosθ)
∴ limθ→0Δ1Δ2=limθ→0sin2θ(1+cosθ)(1−cosθ)
=limθ→0sin2θ(1+cosθ)21−cos2θ
=limθ→0(1+cosθ)2=4
Topper's Solved these Questions
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.1
10 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.2
7 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
From a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View SolutionABCD is a trapezium with AB //DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that: areaof△ADM=areaof△ACN.
View Solution
Knowledge Check
Through each vertex of a triangle, a line parallel to the opposite side is drawn. The ratio of the perimeter of the new triangle, thus formed, with that of the original triangle is
A3:2B4:1C2:1D2:3In a triangle ABC, a line is drawn from C which bisects AB at point D. Find the ratio of area of the triangles DBC and ABC.
 A1:1B2:1C1:2D1:3
A1:1B2:1C1:2D1:3If A=(1,−3)andB=(4,3) are points on the curve y=x−4x then the points on the curve at which the tangents are parallel to the chord AB are
A(1,3),(−3,4)B(±2,0)C(8,142),(16,634)D(1,±3)
In ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
View SolutionPoints A and B are on a circle of radius 5 and AB = 6. Point C is the midpoint of the minor arc AB length of the line segement AC, is:
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionFrom the point (4, 6) a pair of tangent lines are drawn to the parabola, y2=8x. The area of the triangle formed by these pair of tangent lines & the chord of contact of the point (4, 6) is
View Solution
