Find the greatest value of f(x)12ax−x2−5a2∈[−3,5] depending upon the parameter a.
Video Solution
Text Solution
We have f(x)=12ax−x2−5a2=1−4a2−(x−a)2
Let us first draw the graph of y=f(x).
Clearly, f(x) is continuous ∀x∈R.
f(0)=1−5a2. Hence the graph cuts the y-axis at its negative side.
f(a−x)=f(a+x). Hence the graph is symmetrical about the line x = a.
Clearly, y=f(x) is minimum when x=a,f(a)=1−4a2
Also the graph has horizontal asymptote y = 0 (x-axis).
Graph has no vertical or oblique asymptote.
Further f(x)<0,∀x∈R.
From the above information, the graph of y=f(x) is as shown in the following figure.
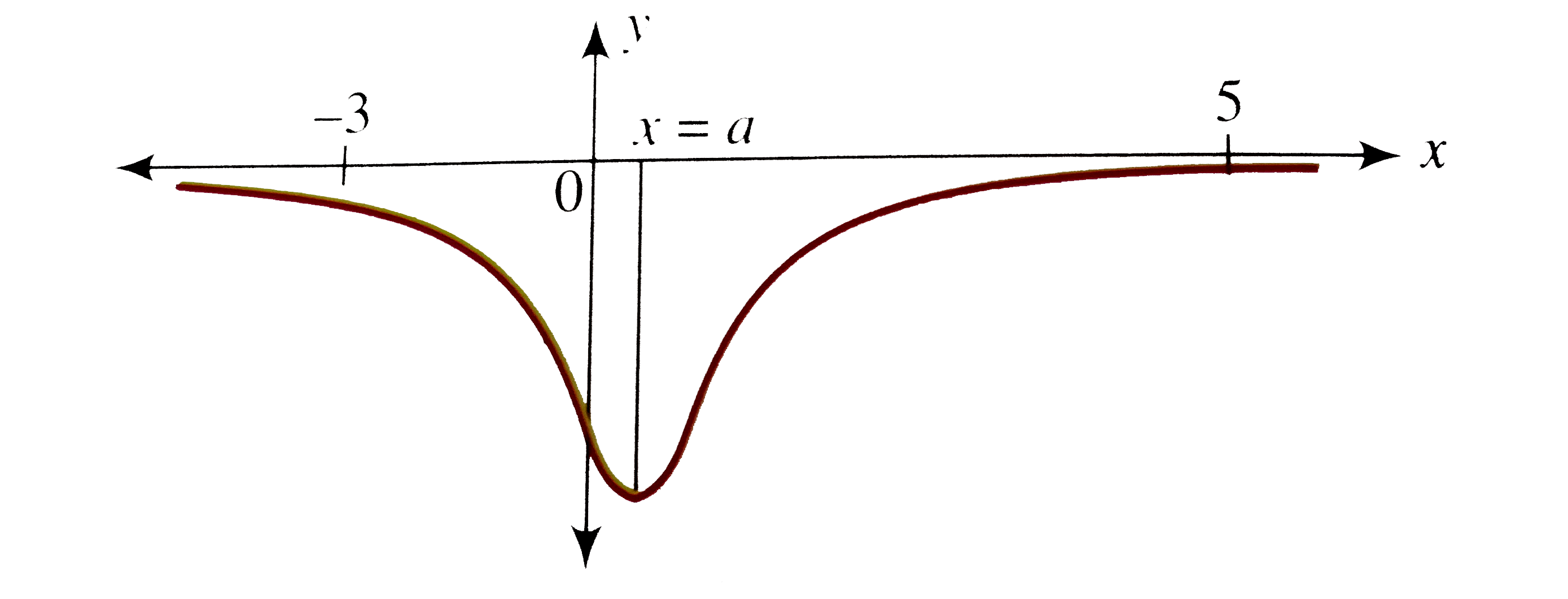
If a=1 (mid point ofx−3andx=5), the greatest value is f(5)=f(−3).
If a<1,fmax(x)=f(5)=−15(a2−2a+5)
and if a>1,fmax(x)=f(−3)=−15a2+6a+9
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
Similar Questions
Knowledge Check
Find the approximate value of f(3.02), where f(x)=3x2+5x+3.
A45.46B37.46C27.56D39.40
Find the greatest and least values of f(x) =x2−12x X∈[−1,3].
View SolutionFind the greatest value of the function f(x)=2√2x2−4x+3
View SolutionFind the approximate value of f(3.12), where f(x)=4x2+5x+2.
View SolutionFind the approximate value of f(3.02), where f(x)=3x2+5x+3.
View Solution7, Find the greatest value of 3+5x−2x2 for all real values of x.
View SolutionFind the approximate value of f(3.02) , where f(x)=3x2+5x+3 .
View SolutionFind the approximate value of f(3.02), where f(x)=3x2+15x+5.
View Solution
