Draw the graph of y=x−1x2 and hence the graph of y=|x−1|x2.
Video Solution
Text Solution
The domain of function is R - {0}.
1. y-intercept
Graph never intersects the y-axis as the domain does not contain x = 0.
2. x-intercept (zeros)
Put y = 0 or x - 1 =0
Hence the graph intersects the x-axis at (1, 0).
3. Asymptotes
Vertical asymptotes
Graph has vertical asymptote x = 0.
Horizontal asymptotes
Since the degree of the denominator is higher than the degree of the denominator , the graph has horizontal asymptote y = 0.
Clearly , the graph has no oblique asymptote.
4. Extremum
f'(x)=2x−x2x4=2−xx3
f'(x)=0⇒x=2
Sign scheme of f'(x) is as follows.
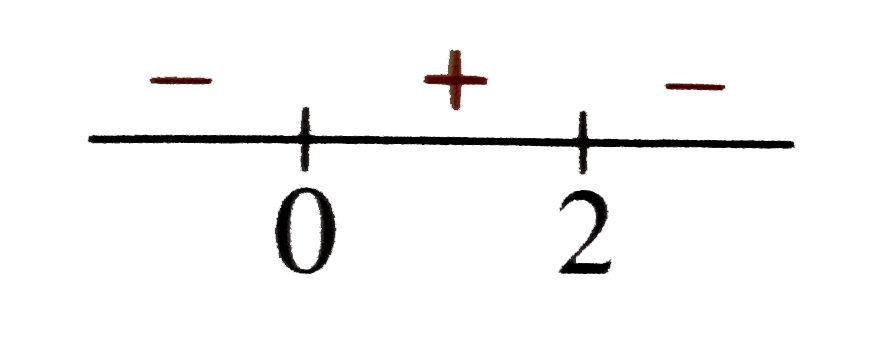
From the sign scheme, x = 2 is the point of maxima.
Also f(2)=14
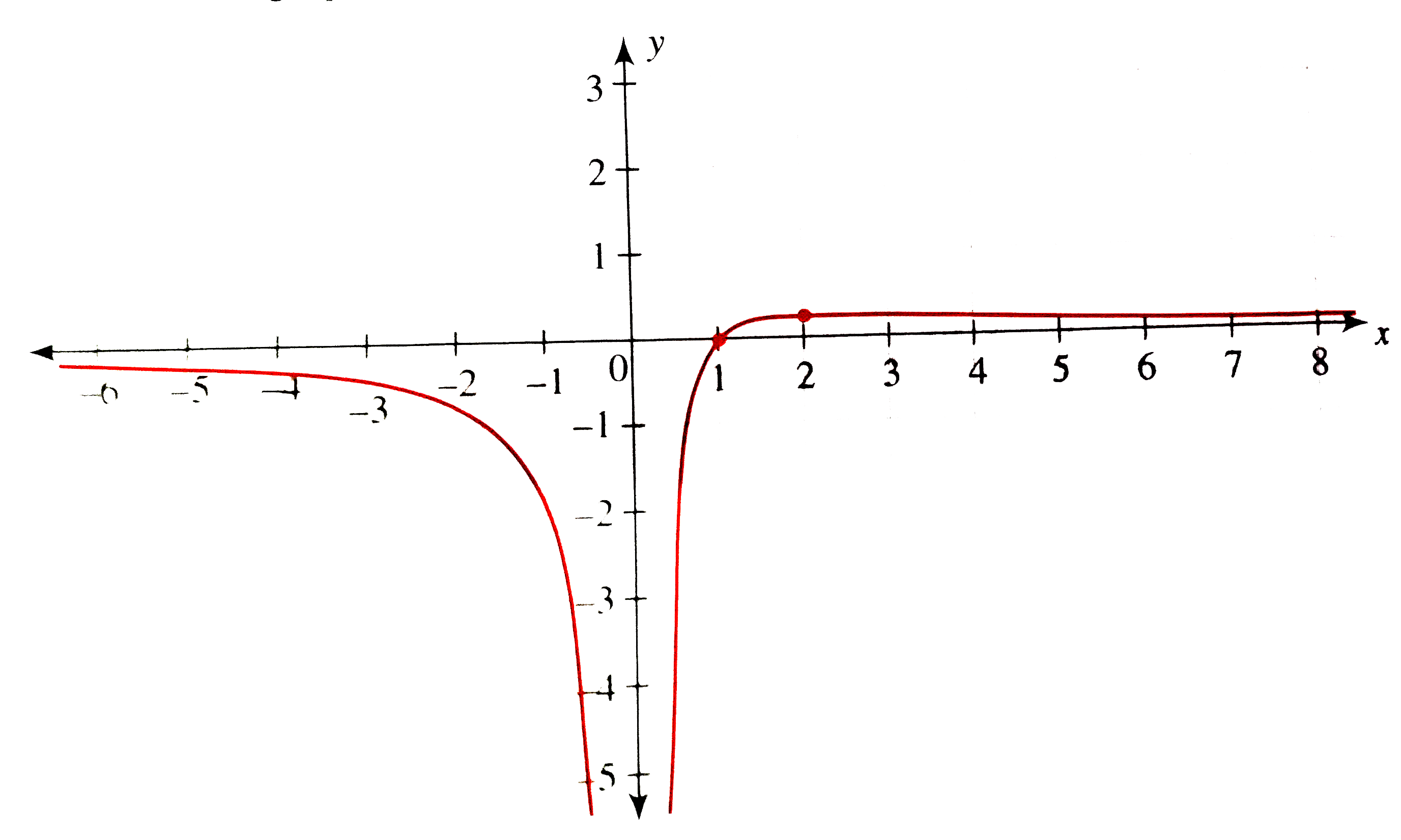
From the above discussion, we have the following reference points and lines.

When x→−∞,y→0 and when x→0−,y→−∞. So f(x) decreases from '0' to '−∞' in (−∞,0).
When x→0+,y→−∞, so f(x) increases from '−∞' ot '1/4', intersecting the x-axis at (1, 0).
f(x) attains the maximum value at x = 2 and then decreases to approach '0' as x approaches '∞' as limx→∞x−1x2=0.
Thus , the graph of y=f(x) is as shown in the following figure.
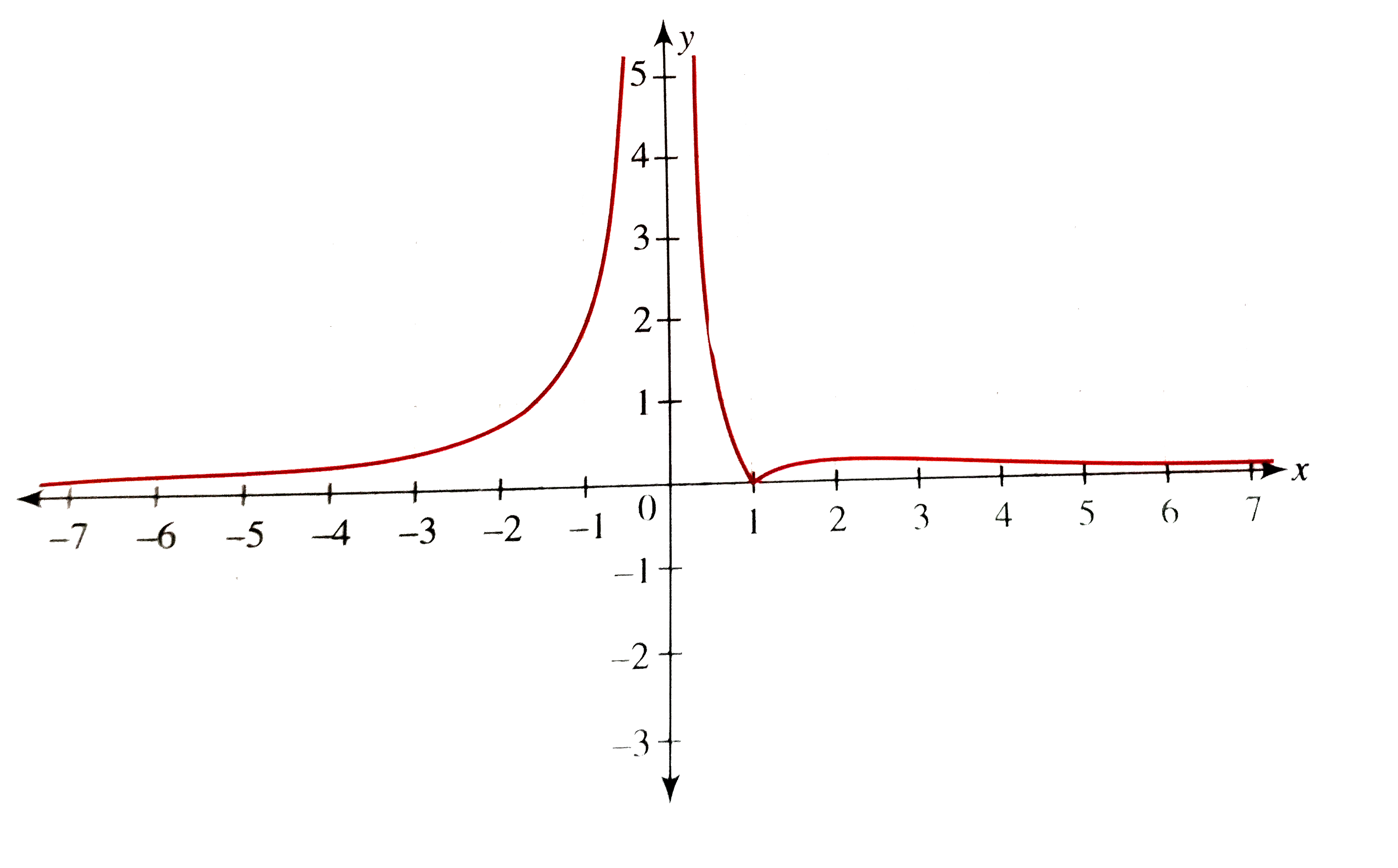
To draw the graph of y=g(x)=|x−1|x2=|f(x)|, flip the portion of the graph which is below the x-axis over the x-axis.
So the graph of y = g(x) is as follows .
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHICAL TRANSFORMATIONSBook:CENGAGEChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
Similar Questions
Draw the graph of y=1x2.
View SolutionDraw the graph of y=2x.
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y≤x+2.
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y=cos−1(x2).
View SolutionDraw the graph of y=|x|+2
View SolutionDraw the graph for |y|=(x−1)(x−2).
View SolutionDraw the graph for y=({x}−1)2.
View SolutionDraw the graph of y=√xx−1
View Solution

