_S01_013_Q01.png)
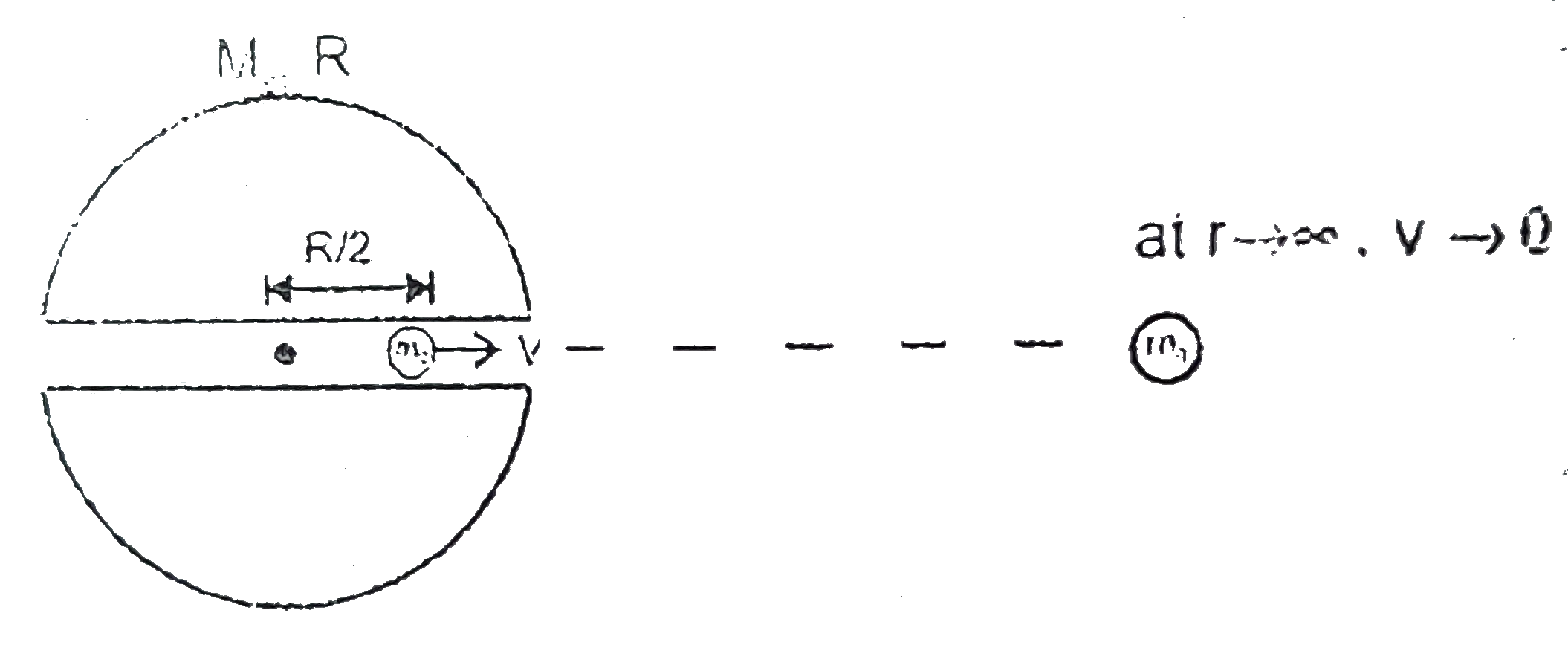
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle for that place.
Suppose we project the particle with speed v so that it just reaches at (r→∞) Applying energy conservation
Ki+Ui=Kf+Uf
12m0v2+m0(−GMe2R3(3R2−(R2)2)=0+0
v=√11GMe4R=Ve at that position
 .
.
Topper's Solved these Questions
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - SOLVED MISCELLANEOUS PROBLEMS
5 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXAMPLE
2 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- NUCLEAR PHYSICSBOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
Similar Questions
_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle fro that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solution
Knowledge Check
A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
Av=ω2(L2−a2)13Bv=ω(L2−a2)Cv=ω2√L2−a2Dv=ω√L2−a2A satellite of mass m is placed at a distance r from the centre of earth (mass M ). The mechanical energy of the satellite is
A−GMmrBGMmrCGMm2rD−GMm2r
Assume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionA semicircular wire hs a length L and mass M. A paricle of mass m is placed at the centre of the circle. Find the gravitational attrction on the particle due to the wire.
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View Solution(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View Solution(a) A uniform rod of mass M and length L is placed at distance L from a point mass m as shown. Find force on m
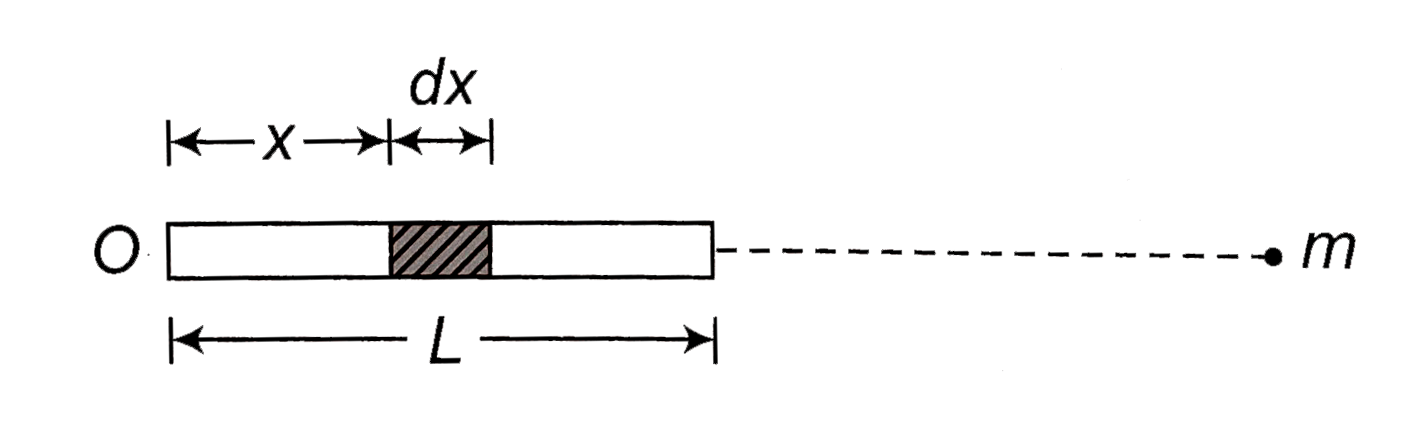
(b) A semiconductor wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. find the gravitational attraction on the particle due to the wire.
View Solution
