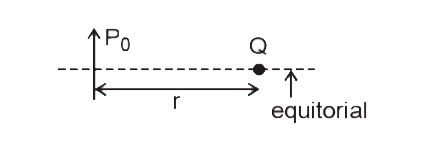
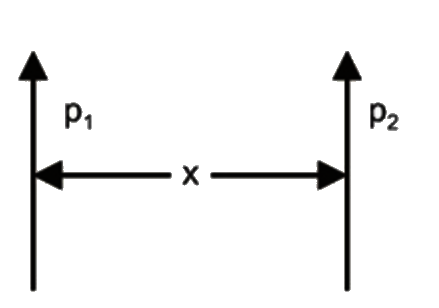
Find force on short dipole P2 due to short dipole P1 if they are placed at a distance r a part shown in figure.

Force on P2 due to P1
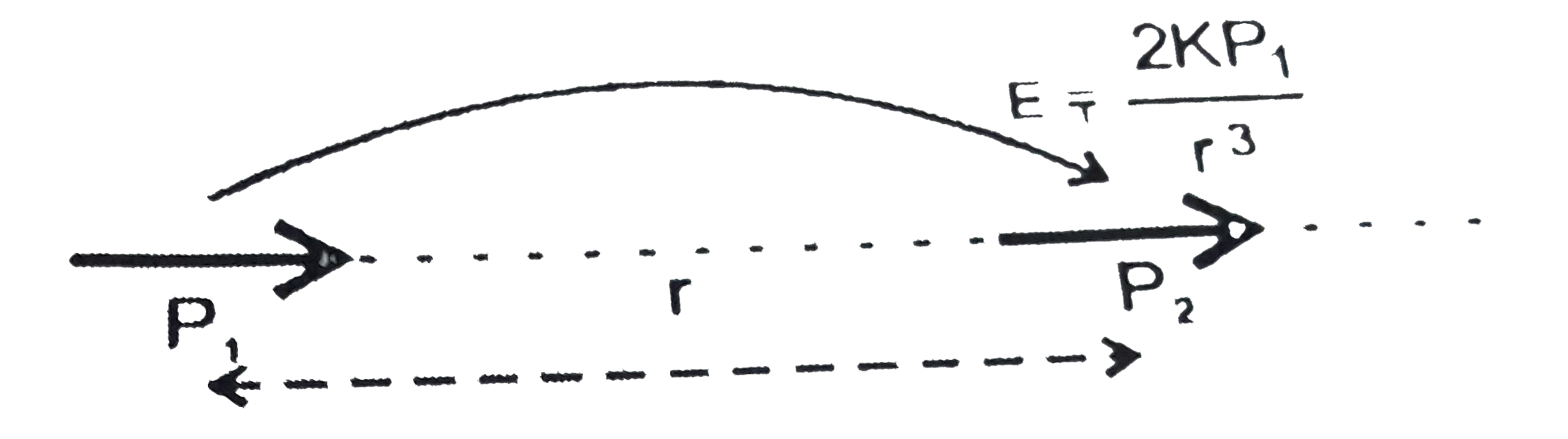
F2=(P2)(dE1dr)
∴F2=(P2)(ddr(2kP1r3)) or F2=−6KP1P2r4
Here - sign indicates that this force will be attractive (opposite to r)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Knowledge Check
Electric potential V due to a short dipole is related to the distance r of the observation point as
AV∝rBV∝r−1CV∝r−3DV∝r−2In a system of two dipoles placed in the way as shown in figure :
 AIt is possible to consider a spherical surface of radius a and whose centre lies within the square shown through which total flux is +veBIt is possible to consider a spherical surface of their a and whose centre lies within the square shown through which total flux is −veCIt is possible to consider a spherical surface of radius a and whose centre lies within the square shown through which total flux is zeroDThere are two points within the square at which EF is zero.
AIt is possible to consider a spherical surface of radius a and whose centre lies within the square shown through which total flux is +veBIt is possible to consider a spherical surface of their a and whose centre lies within the square shown through which total flux is −veCIt is possible to consider a spherical surface of radius a and whose centre lies within the square shown through which total flux is zeroDThere are two points within the square at which EF is zero.Two short dipoles , each of dipole moment P are placed at a large separation r. The force between them
Ais proportional to product of dipole momentaBis inversely proportional to r4Cthe force is attractive , if direction of dipole momenta are same , repulsive if oppositeDall options are correct
Find out force experienced by short dipole →P0 is following different arrangements as shown in figures. [Assume point charge is Q,→P0=q0and→P=q(2a)]
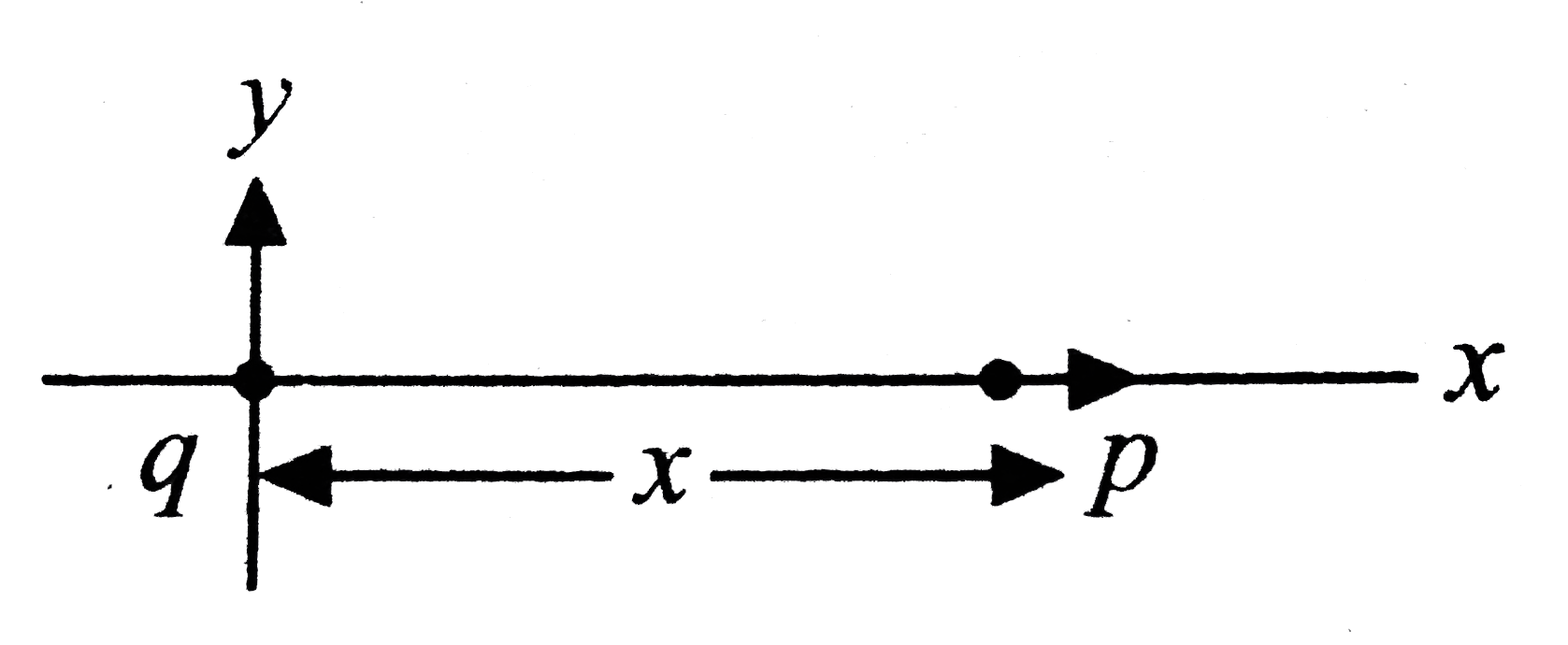
View SolutionA short dipole is placed along the x - axis at x=x (Fig. 3.120).
 .
.
a. Find the force acting on the dipole due to a point charge q placed at the origin.
b. Find the force on the dipole if the dipole is rotated by 180∘ about the z- axis.
c. Find the force on dipole if the dipole is rotated by 90∘ anticlockwise about z - axis, i.e., it becomes parallel to the y - axis.
View SolutionEstablish a relation for electric potential due to short dipole at a point distance r from the dipole along a line inclined at an angle θ from the dipole axis . Hence obtain value of electric potential at a point lying along (i) axial line , (ii) equatoral line of the dipole .
View SolutionFind the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
View SolutionFour short dipoles each of dipole moment 'p' are placed at the vertices of a square of side a. The direction of the dipole moments are shown in the figure.

View Solution