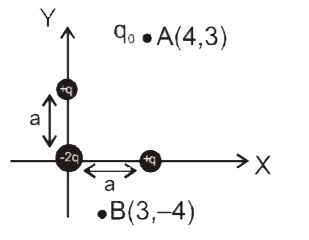
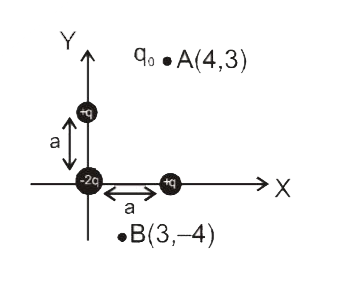
(i) Find potential at point A and B sue to the small charge - system fixed near origin. (Distance between the charges is negligible).
(ii) Find work done to bring a test charge q0 from point A to point B, slowly. All parameters are in S.I. units.
Video Solution
Text Solution
(i) Dipole moment of the system is →P=(qa)ˆi+(qa)ˆj
Potential at point a due to the dipole
VA=K(→P.→r)r3=K[(qa)ˆi+(qa)ˆj].(4ˆi+3ˆj)53=k(qa)125(7)
⇒VB=K[(qa)ˆi+(qa)ˆj](3ˆi−4ˆj)(5)3=−K(qa)125
(ii) WA→B=UB−UA=q0(VB−VA)=q0[−K(qa)125−(K(qa)(7)125)]
⇒WA→B=−Kqq0a125(8)
|
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Knowledge Check
If 6W is the work done in bringing a infinitesimal small test charge 6g from infinity to a point P, then potential at point P is
AδWδqB−δWδqC−δW.δqDNone of theseThe potential at a point is 20 V. The work done in bringing a charge of 0.5 C. from infinity to this point will be
A20 JB10 JC5 JD40 JThe electirc field strength at a distance r from the centre of a charged sphere of radius r is E. If r>R, how much work will be done in bringing a test charge q0 from infinity to that point, is
Aq0REB12q0RECq0rED12q0rE
Find an expression for the potential at a point due to a point charge Q.
View SolutionThe electrical potential at point in an electric field is 6 V. Find the work done in bringing 12 C of charge from infinity to that point.
View SolutionFind out potential at P and Q due to the two point mass system Find out work done by external agent in bringing unit mass from P to Q Also find work done by gravitational force.
 .
.
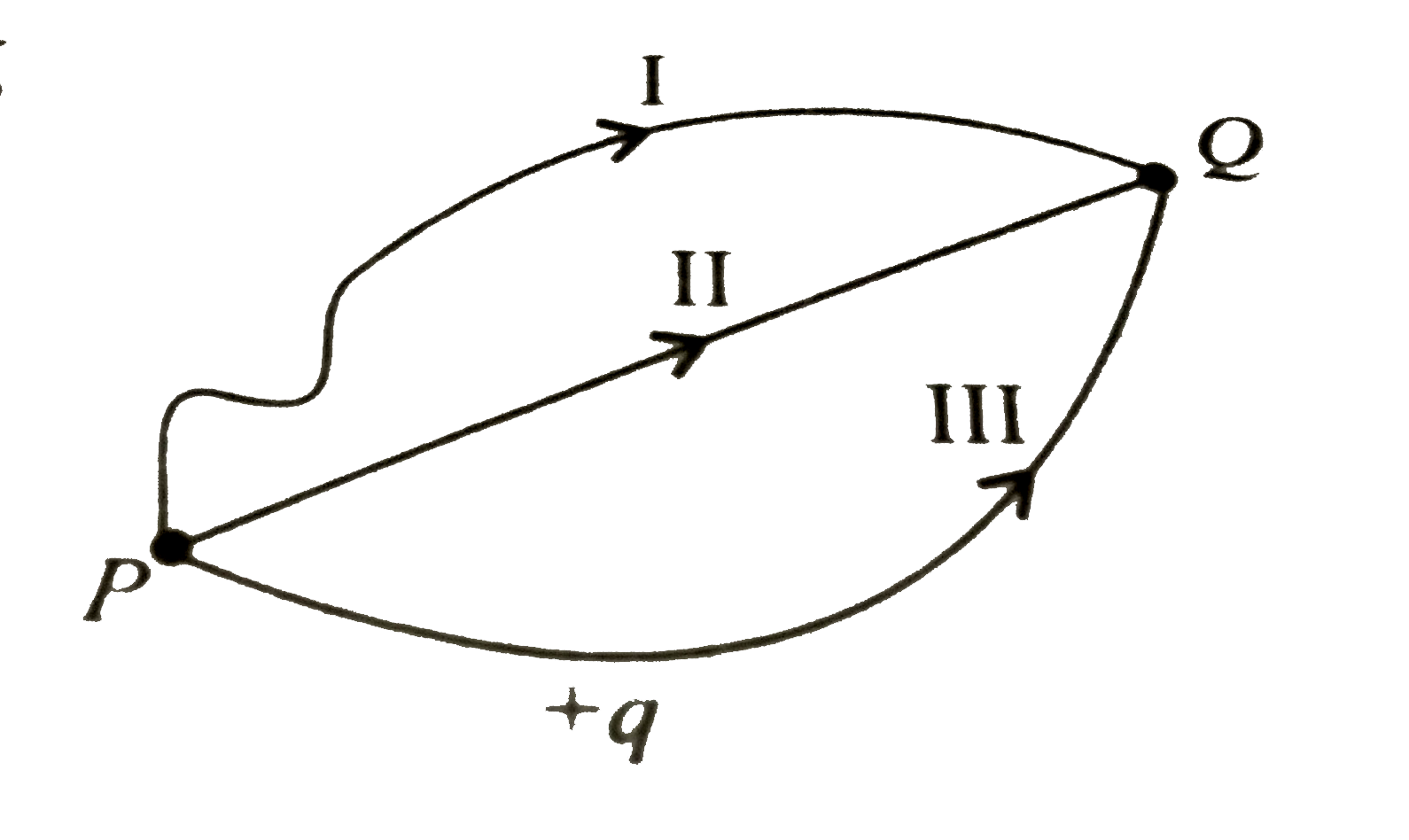
View SolutionWhich among the following statements is true about the work done in bringing a unit positive charge from point P to Q in an electrostatic field ?
View SolutionThe work done in bringing 5 C of charge from infinity to a point A near a charged body is 20 J. Find the potential at point A.
View Solution