Determine and draw the graph of electric field due to infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ as a function of distance x from its symmetry plane.
(a) x<t2 (b) x≥t2
We can consider two sheets of thickness (t2−x) and (t2+x)
Where the point P lies inside the sheet.
Now, net electric feld at point P :
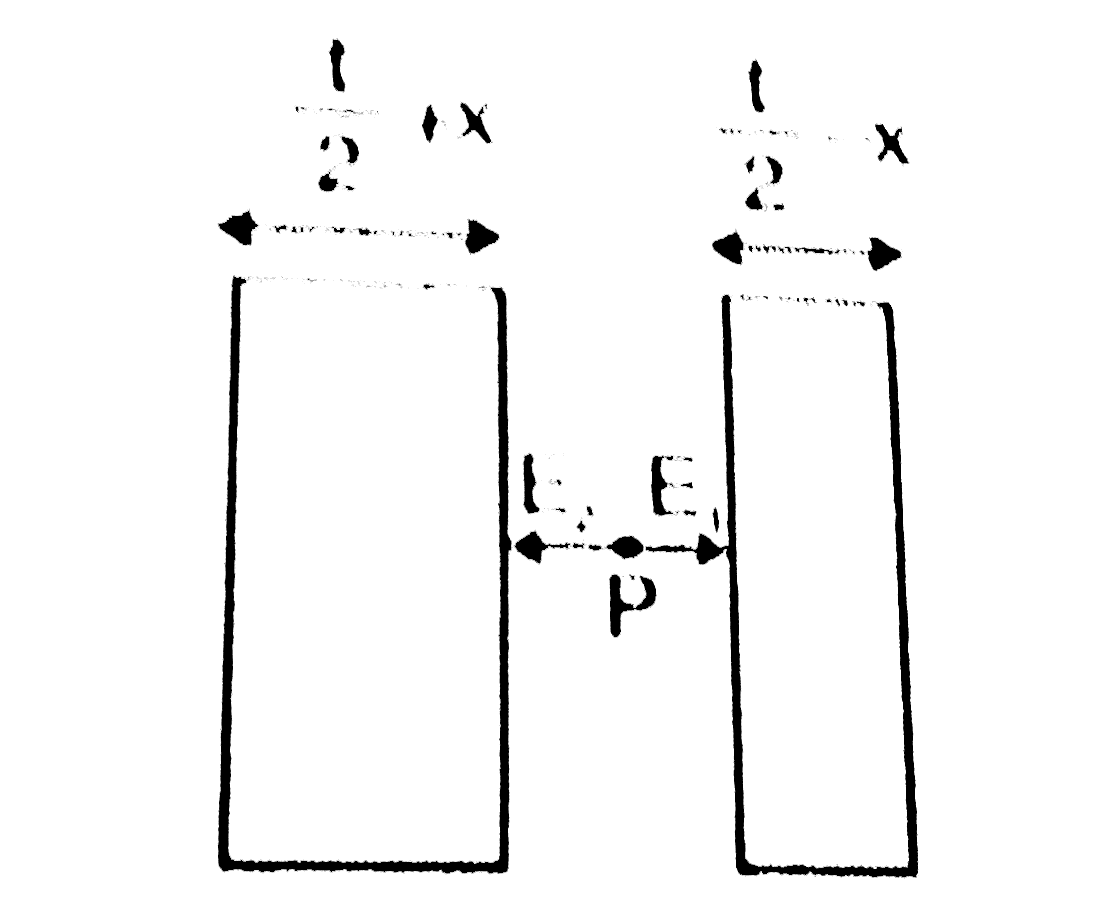
E=E1−E2=Q12Aε0−Q22aε0[Q1 : Charge of left sheet, Q2 : charge of right sheet.]
=Aρ(t2+x)−ρA(t2−x)2Aε0=ρxε0
For point which lies outside the sheet we can consider a complete sheet of thickness t
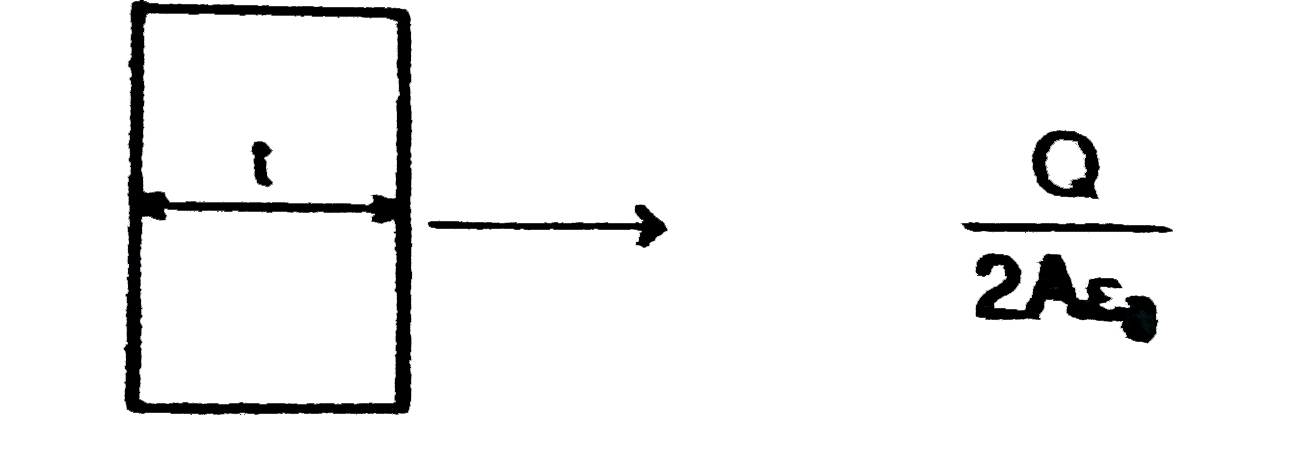
E=σtA2aε0=σt2ε0
Alternate : We can assume thick sheet to be made of large number of uniformly charged thin sheets. Consider an elementary thin sheet of width dx at a distance x from symmetry plane.
charge in sheet =ρAdx (A : assumed area of sheet)
surface charge density, σ=ρAdxA
So, electric field intensity due to elementary sheet : dE=ρdx2ε0
(a) When x<t2⇒ ENet=x∫−t/2ρdx2ε0−t/2∫xρdx2ε0=ρxε0
(b) When x>t2⇒ ENet=t/2∫−t/2ρdx2ε0=ρt2ε0

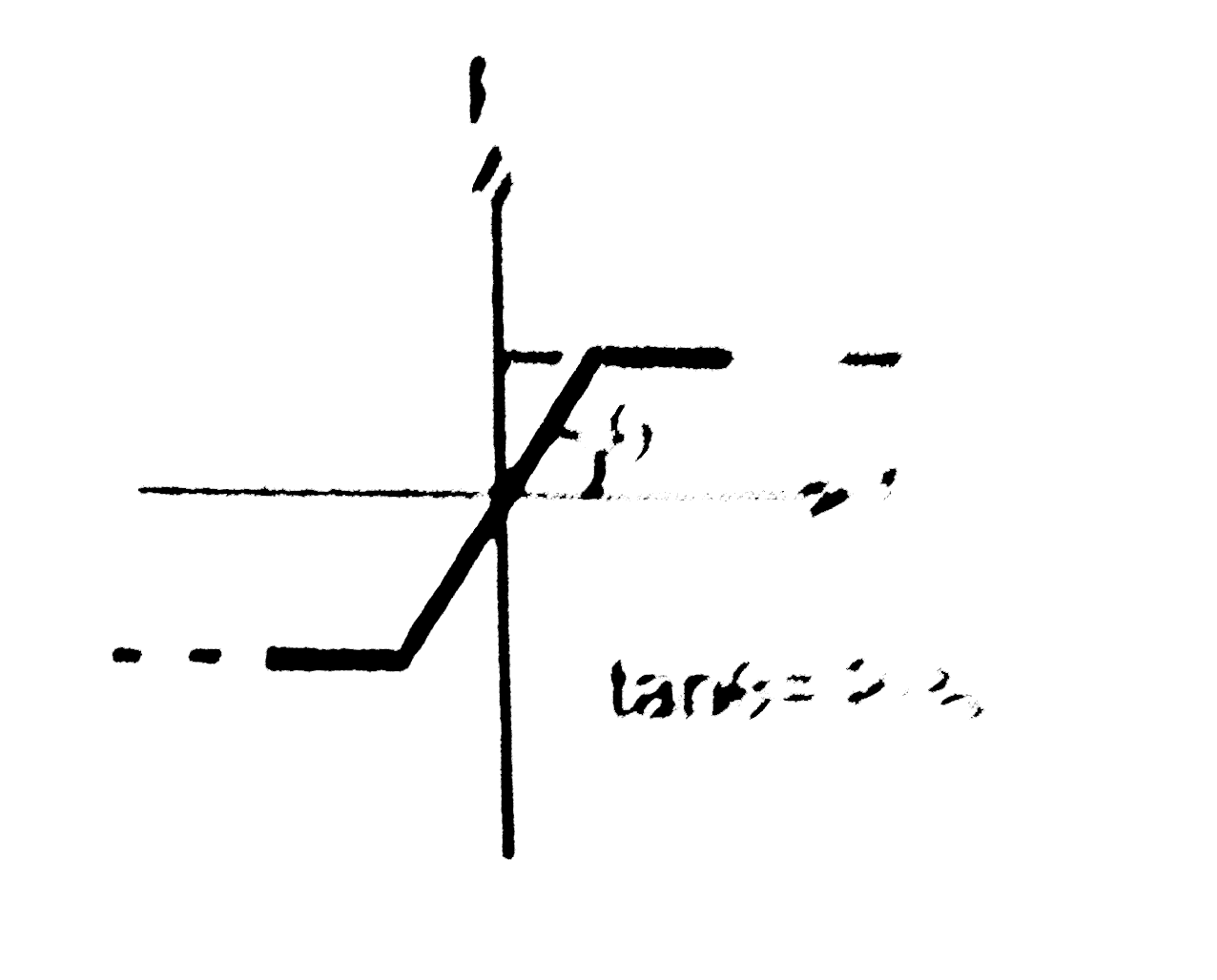
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionAn infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ is given in which left half og the sheet contains charge density ρ and right half contains charge density. Find the electric field at the symmetry plane of this sheet
View Solution
Knowledge Check
Two infinite parallel,non- conducting sheets carry equal positive charge density σ ,One is placed on the other at distance x=a Take potential V=0 at x=0 then
AFor 0≤x≤a potential Vx=0Bfor x≥a potential Vx=σε0(x−a)Cfor x≥a potential Vx=−σε0(x−a)DFor x≤a potential Vx=−σε0x
Find out electric field intensity due to uniformly charged solid non-conducting sphere of volume charge density ρ and radius R at following points :
(i) At a distance r from surface of sphere (inside)
(ii) At a distance r from the surface of sphere (outside)
View SolutionThe electric potential at surface of thin non-conducting sheet with charge density σ is V0. Show that the electric potential at a distance x from infinite sheet can be written as
V=V0−σ2∈0x
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionA block having mass m and charge Q is resting on a frictionless plane at a distance d from fixed large non-conducting infinite sheet of uniform charge density −σ as shown in Figure. Assuming that collision of the block with the sheet is perfectly elastic, find the time period of oscillatory motion of the block. Is it SHM ?
View SolutionThe potential in the electric field varies as V=−ax2+b with respect to x - coordinate, where a and b are constants. Find the charge density ρ(x) in a space.
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0<x<<d.
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0<x<<d.
View Solution