A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.

Video Solution

Text Solution

Verified by Experts

Consider an element of small angle $d ϕ$ at an angle $ϕ$ as shown.
Soordinates of element : $(R cos ϕ, R sin ϕ, 0)$
Coordinates of point : (0, 0, x)
Now electric field due to element :

$- \to d E = \frac{K (λ R d ϕ) . [- R cos ϕ ˆ i - R sin ϕ ˆ j + x ˆ k]}{{(R^{2} {cos}^{2} ϕ + R^{2} {sin}^{2} ϕ + x^{2})}^{3 / 2}} \Rightarrow E_{x} = Σ d E_{x} = - π \int 0 \frac{K λ R^{2} cos ϕ d ϕ}{{(R^{2} + x^{2})}^{3 / 2}} = 0$
$E_{y} = Σ d E_{y} = - π \int 0 \frac{K λ R^{2} sin ϕ d ϕ}{{(R^{2} + x^{2})}^{3 / 2}} = \frac{2 K λ R^{2}}{{(R^{2} + x^{2})}^{3 / 2}} = \frac{2 K Q R}{π {(R^{2} + x^{2})}^{3 / 2}}$
$E_{z} = Σ d E_{z} = π \int 0 \frac{K λ R x d ϕ}{{(R^{2} + x^{2})}^{3 / 2}} = \frac{K Q x}{{(R^{2} + x^{2})}^{3 / 2}}$
$E_{net} = \sqrt{E_{x}^{2} + E_{y}^{2} + E_{z}^{2}} = \frac{K Q}{{(R^{2} + x^{2})}^{3 / 2}} \sqrt{\frac{4 R^{2}}{π^{2}} + x^{2}}$
alternate solution :

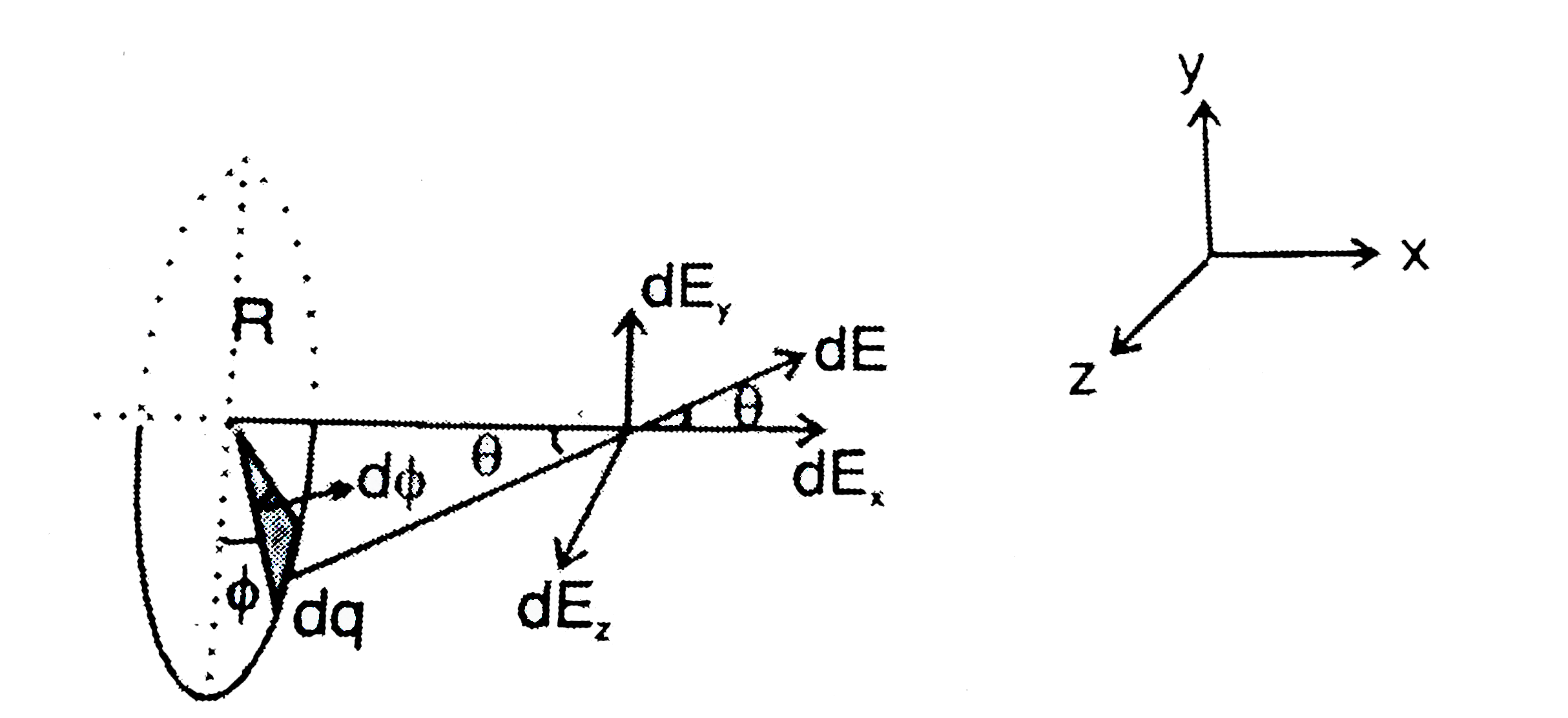
Consider an element of charge dq at an angle $ϕ$ on circumference of half ring. Due to this element electric field at the point on axis, which is at a distance x from the centre of half ring is dE. This electric field can be resolved into three component.

$E_{Z} = π / 2 \int - π / 2 d E sin θ sin ϕ = 0$
$E_{X} = π / 2 \int - π / 2 d E cos θ = \frac{K Q x}{{[R^{2} + x^{2}]}^{3 / 2}}$ ...(1)
$E_{Y} = π / 2 \int - π / 2 d E sin θ cos ϕ = \int \frac{K d q}{R^{2} + x^{2}} sin θ . cos ϕ = \frac{2 K λ R sin θ}{R^{2} + x^{2}}$ ...(2)
$∴ d q = λ R d ϕ, sin θ = \frac{R}{\sqrt{R^{2} + x^{2}}} \Rightarrow E_{net} = \sqrt{E_{X}^{2} + E_{Y}^{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

RESONANCE-ELECTROSTATICS-HLP

Home
Ask Doubt
Profile