Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed ω=40rad/s,B=0.10T and R=1Ω. The current through the resistor is
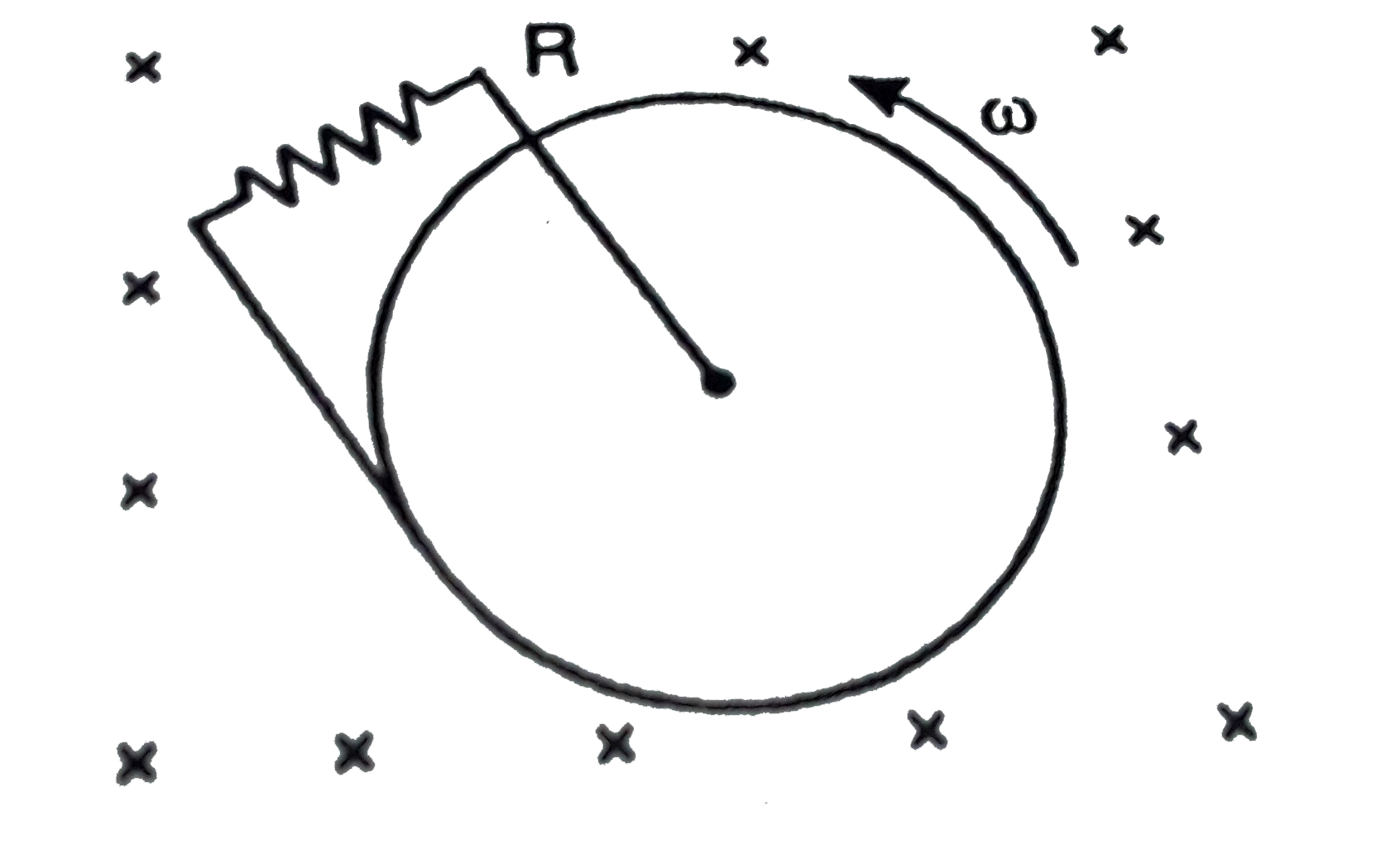
5mA
50A
5A
10mA
The correct Answer is:A
Step by step video, text & image solution for Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed omega=40 rad//s, B=0.10 T " and " R=1 Omega. The current through the resistor is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The following figure a conducting disc rotating about its axis in a perpendicular magnetic field B. The resistor of resistance R is connected between the centre and the rim. The current in the resistor is (The radius of the disc is 5.0 cn=m, angular speed ω=10rads−1,B=0.40TandR=10Ω)
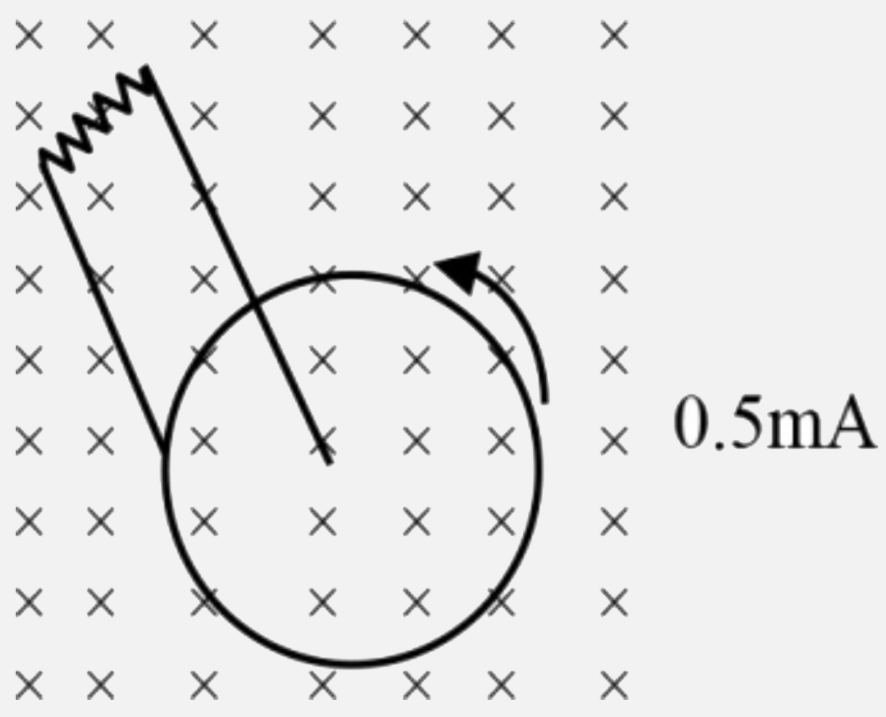
View SolutionA copper disc of radius 10 cm rotates 20 times per scond with its axis parallel to a uniform magnetic field of 0.5 tesla . Calculate the induced emf between the centre and the edge of the disc.

View Solution
Knowledge Check
A non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23A circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
AπωBR2BωBR2CπωBR22DωBR2/2A circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
AπωBR2BωBR2CπωBR22DωBR2/2
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View Solutiona copper disc of diameter 20cm makes 1200 r.p.m. about its natural axis kept parallel to a uniform magnetic field of 10−2T. The potential difference between the centre and edge of the disc is
View Solutiona conducting disc of radius R roatates about its axis when an angular velocity ω.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
View SolutionRadius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
View Solution