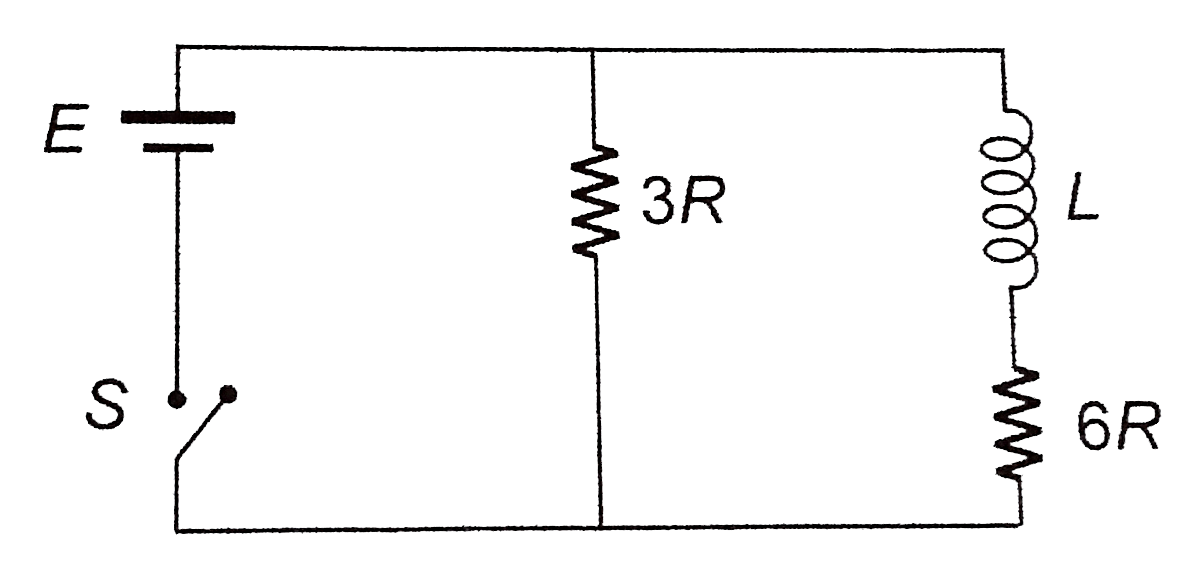
At t=0, switch S is closed (shown in Fig.). After a long time, suddenly the inductance of the inductor is made η times lesser (L/η) than its initial value. Find out current just after the operation.

Using above result (note 4)
L1i1=L2i2⇒i2=ηεR
Similar Questions
Knowledge Check
In Fig. switch S is closed for a long time. At t=0, if it is opened, then
 Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1After switch S2 is closed and S1 is opened, the maximum value of current through the inductor is:
A(√CL)EB(√C2L)EC(√3C2L)ED(√5C4L)EIn the circuit shown in figure switch S is closed at time t=0
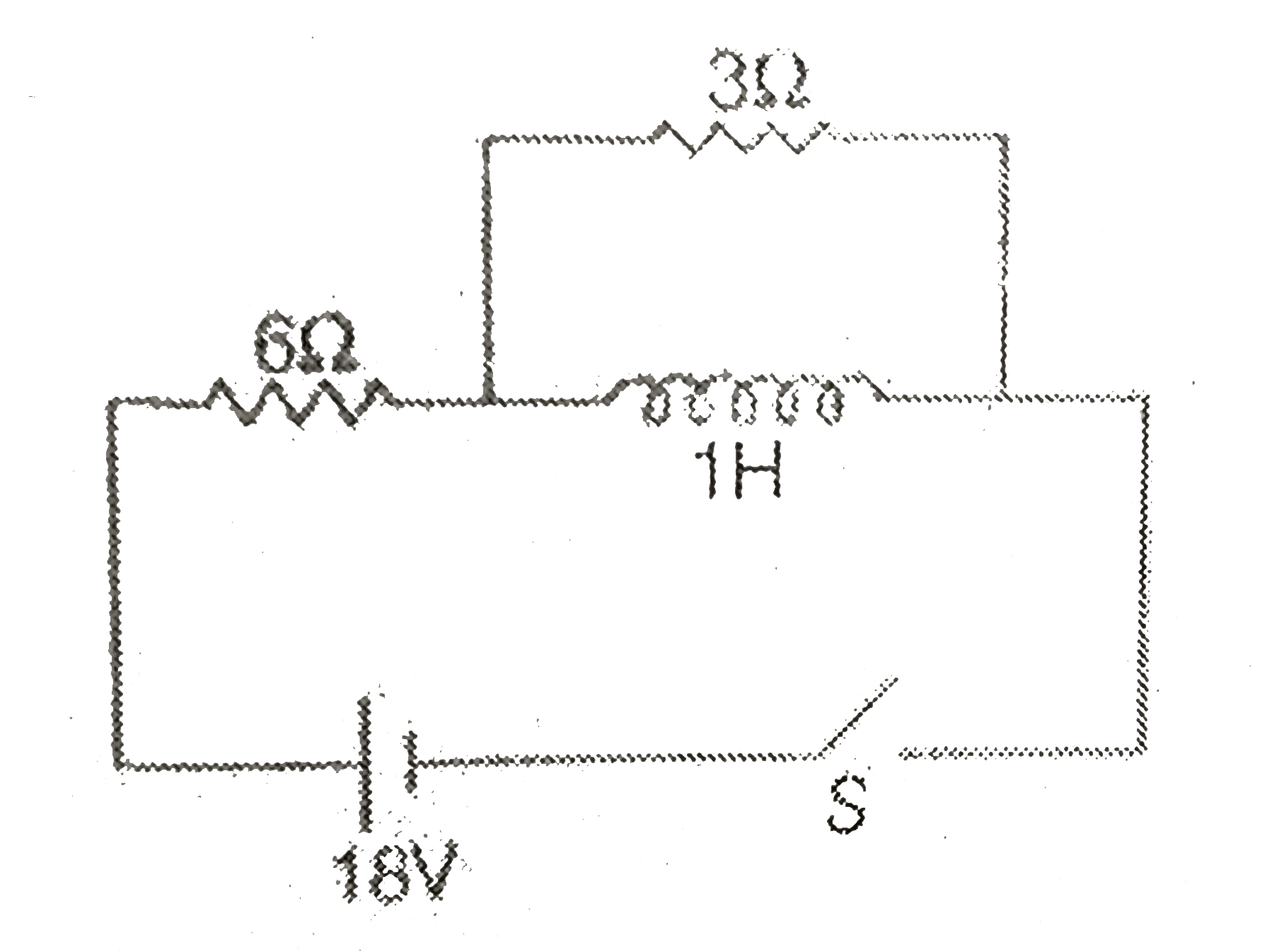
At what time current through 3Ω resistance and 1H inductor are equal?AIn√53BIn(83)CIn(53)DIn√83
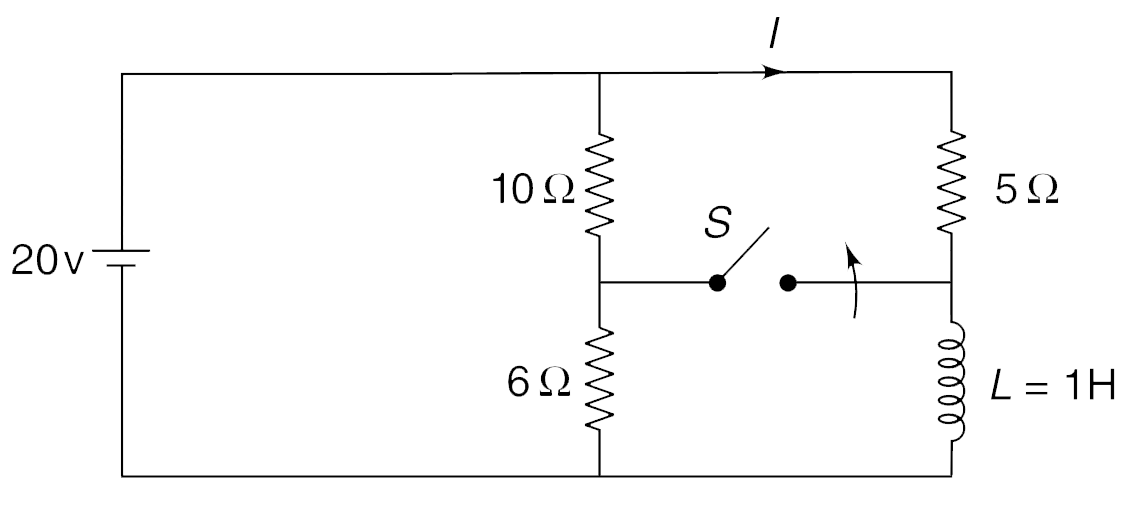
In the circuit shown, the switch ‘S’ has been closed for a long time and then opens at t = 0.
(a) Find the current through the inductor just before the switch is opened.
(b) Find the current I a long time after the switch is opened.
(c) Find current I as a function of time after the switch is opened. Also write the current through the cell as a function of time.
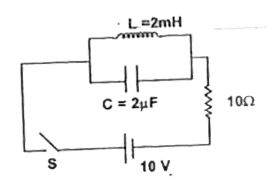
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionAt t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out

Charge on the capacitor long after that moment.
View SolutionThe switch is closed for a long time and then opned at time t=0 . Find the initial voltage across L after t=o , which end is at higher potential a or b ?

View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
View Solution