A ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

At any time, ϕ=BAcosθ=BAcosωt
Now induced emf in the loop

e=−dϕdt=BAωsinωt
If there are N turns.
emf=BAωNsinωt
BAωN is the amplitude of the emf
e=emsinωt
i=eR=emRsinwt=imsinwt
im=emR
The rotating coil thus produces a sinusoidally varying current or alternating current. This is also the principle used in generator.
Similar Questions
A ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.

View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
AIt is rotated about it axisBit is translatedCit is rotated about a diameterDit is deformed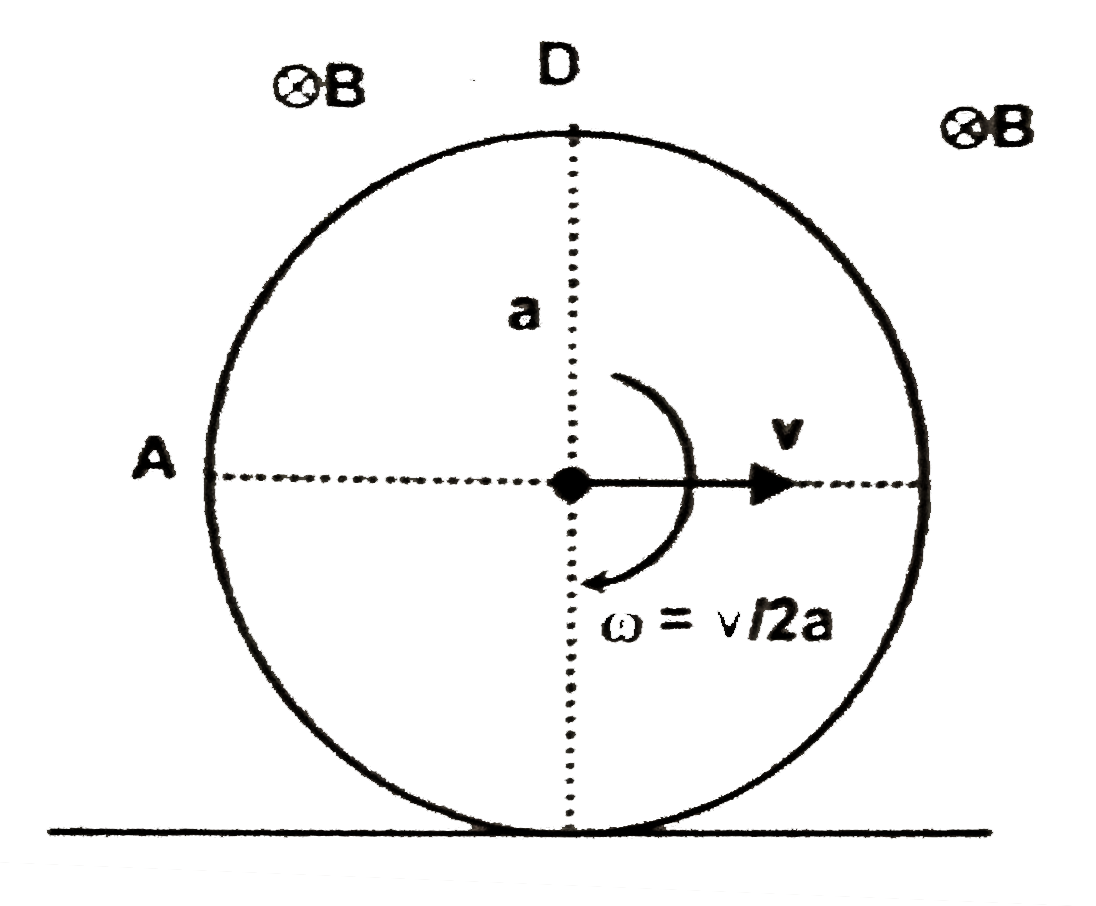
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring isABωa2B2Bωa2C4Bωa2D6Bωa2From a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,A912MR2B1112MR2C11.312MR2DMR2
,A912MR2B1112MR2C11.312MR2DMR2
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionIn the figure there are two identical conducting rods each of length a rotating with angular speed ω is the direction shown.One end of each rod touches a conducting ring.Magnetic field B exists perpendicular to the plane of the rings.The rods the conducting rings and the lead wires and resistanceless.Find the magnitude and direction of current in the resistance R.
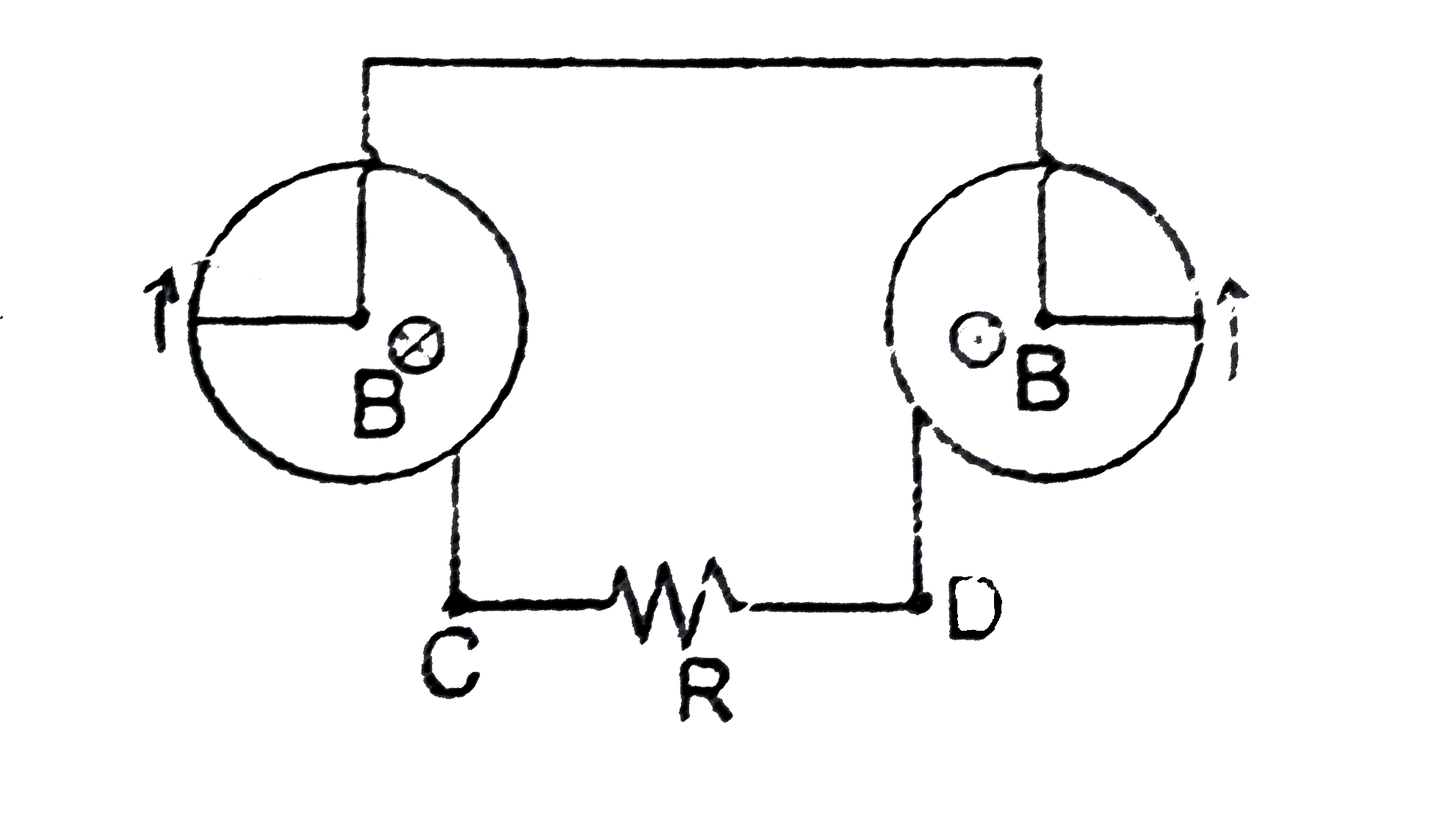
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionA thin non-conducting ring of mass m carrying a charge q can freely rotate about its axis. At the initial moment, the ring was at rest and no magnetic field was present. Then a uniform magnetic field was switched on, which was perpendicular to the plane of the ring and increased with time according to a certain law: dBdt=k.
Find the angular velocity ω of the ring as a function of k.
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
View Solution
