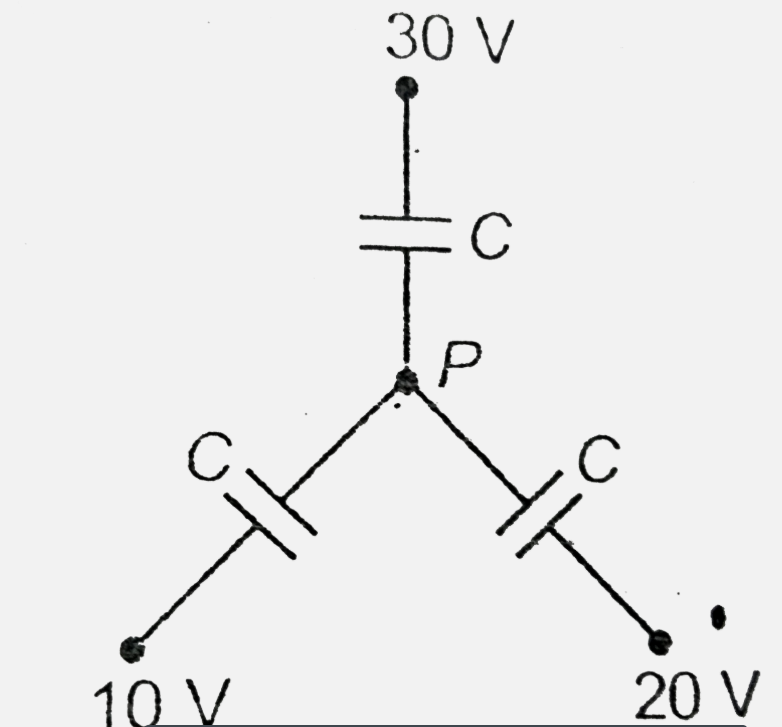
Find the potential at point A

Let potential at A=x, applying Kirchhoff current law at junction A
x−20−101+x−15−202+x+301=0
2x−60+x−35+x+45+2x+602=0
⇒6x+10=0⇒x=−5/3
Potential at A=−53V
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Solued miscellaneous Prolblems
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-1)
Explore 46 Videos
- COMMUNICATION SYSTEMSBook:RESONANCEChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
Similar Questions
The arrangement shows a part of complete circuit. The potentials at point A and B are V1 and V2 respectively . Find the potential at point P.
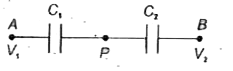
Strategy : The two capacitors C1 and C2 are connected in series . Therefore the charge on both of the capacitors is same . Let the potential at P is V .
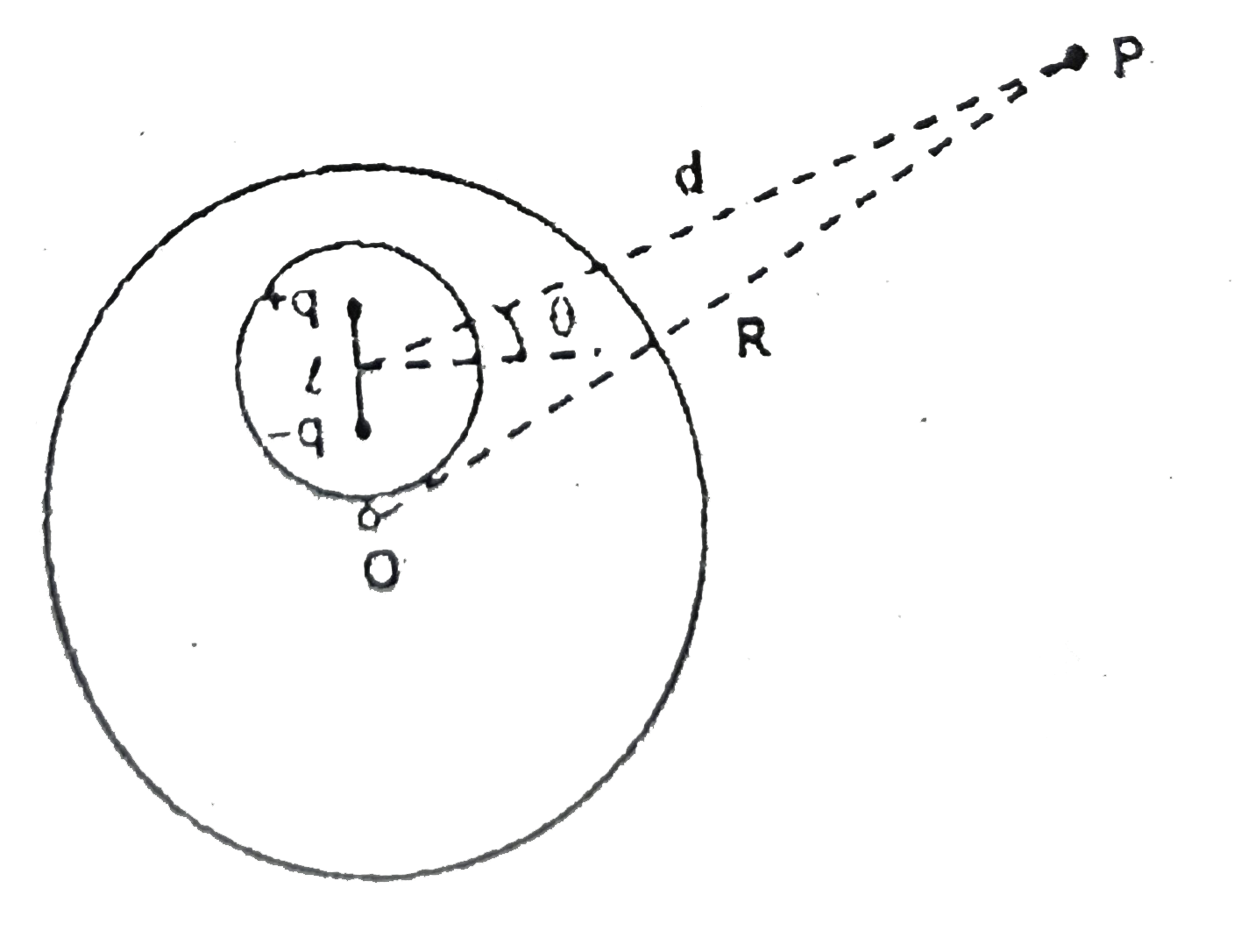
View SolutionA cavity is taken out from a uniform conducting sphere. Inside the cavity a dipole is placed as shown in the figure. Find the potential at point P (in Volt).
(q=10−8C, l=0.1mm, θ=30∘, d=10cm, R=12cm)
View Solution
Knowledge Check
In the following circuit , find the potentials at points A and B is.
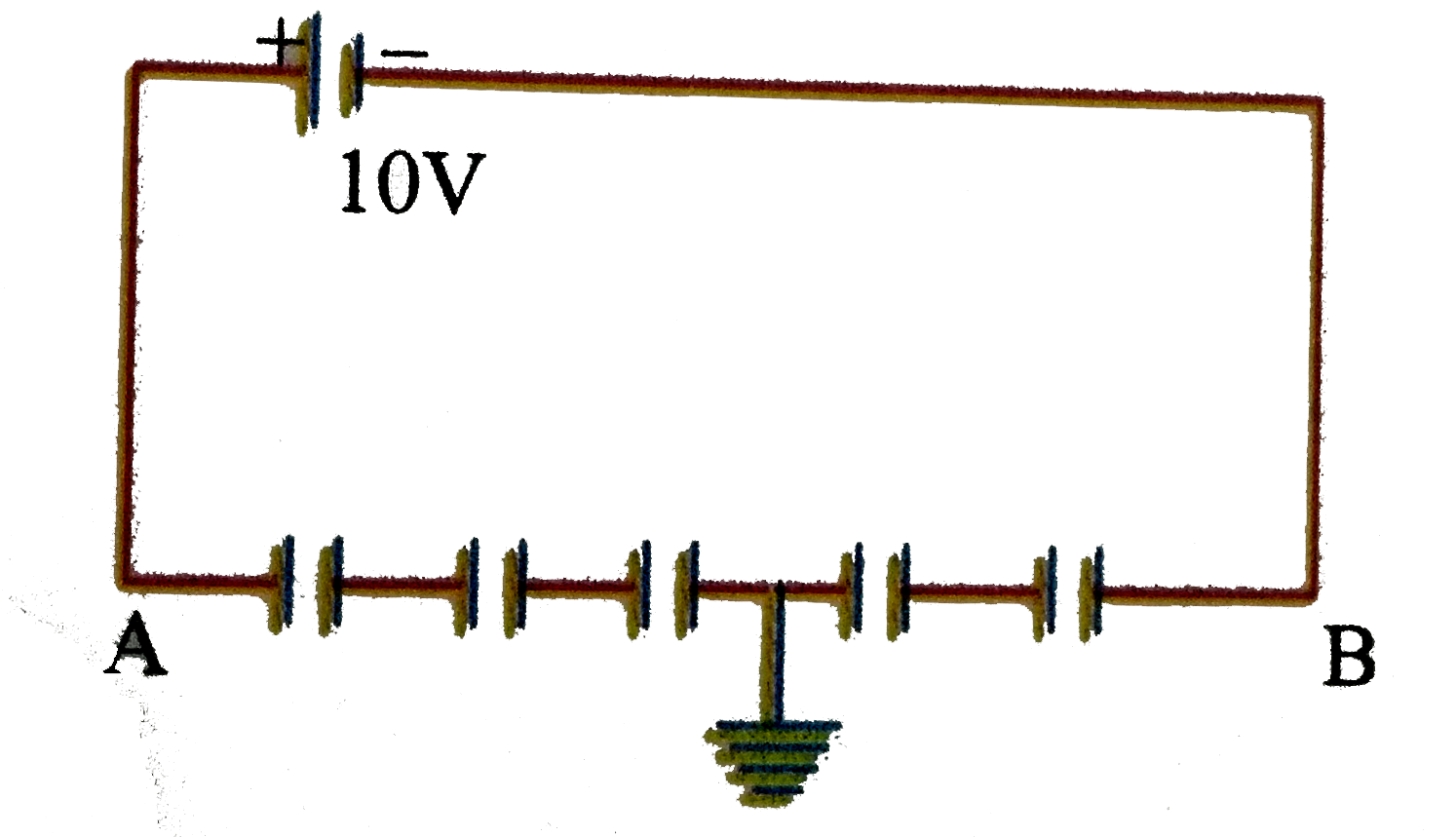 .A10 V,0VB6V,−4VC4V,−6VD5V,−5V
.A10 V,0VB6V,−4VC4V,−6VD5V,−5VThree spherical shells of masses M, 2M and 3M have radii R, 3R and 4R as shows in figure. Find net potential at point P, where CP=2R.
 A−13GM12RB−23GM6RCzeroD−23GM12R
A−13GM12RB−23GM6RCzeroD−23GM12R
Find the potential of point P
View SolutionIn the electrical circuit shown, points B and C are earthed . Find the potentials of points A and D .
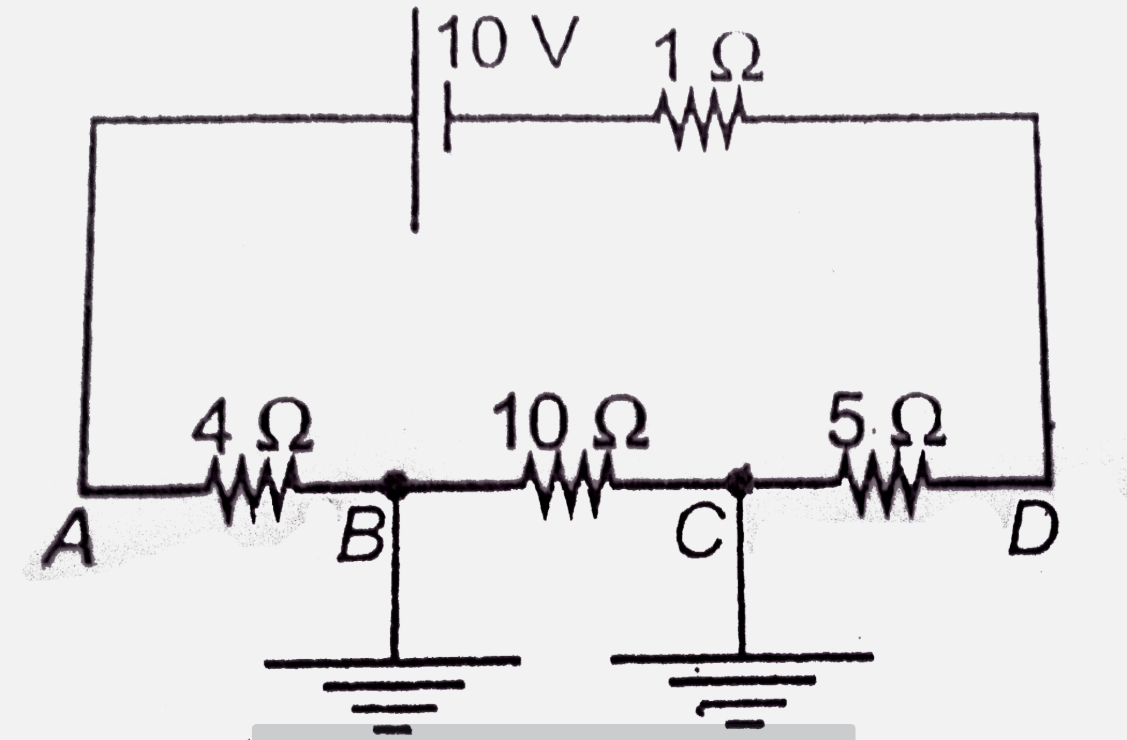
View SolutionIn the given circuit both diodes are ideal having zero forward resistance and built-in potential of 0.7 V. Find the potential of point E in volts.
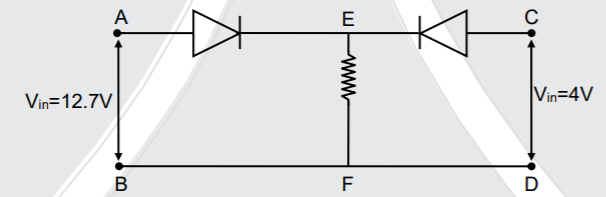
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFind potential at point A and B due to the small charge -system fixed near origin. (distance between the charges is negligible).
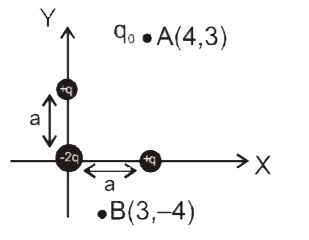
View SolutionThe work done in moving a charge of 2×10−9 C from a point of potential - 3000 V to another point P is 5×10−5J . Find the potential at the point P.
View Solution

