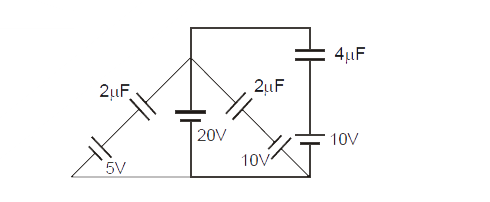
If A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
Video Solution
Text Solution
Let potential of B and c is zero and common potential on capacitors is V, then at A and D it will be V
2V+3V=10⇒V=2 volt
Now charge on each plate is shown in the figure
Heat produced =400+150−12×5×4=550−10=545μJ
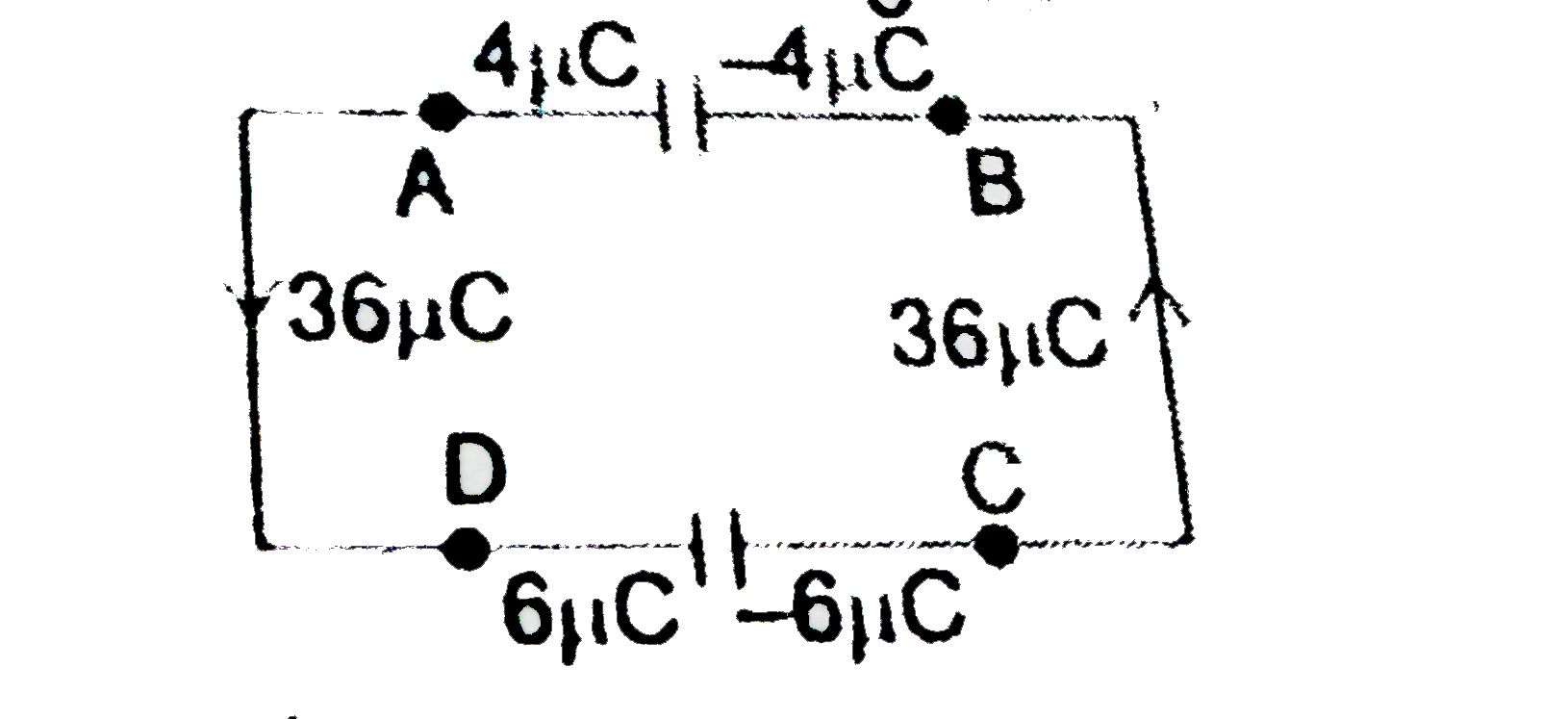
Note : Here heat produced is more. Think why ?
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example3videos
CAPACITANCE
- BOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Exercise - 179videos
CAPACITANCE
- BOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
- BOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two capacitors C1 and C2 are charged separately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectively. A is connected with CandB is connected with D.
i. Find the final potential difference across each capacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.A128μC 142μC 60uJB28μC 42μC 60uJC28μC 42μC 160uJD2.8μC 4.2μC 60uJ
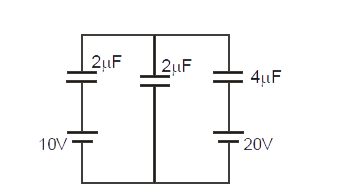
Find charge in each capacitor:
View SolutionFind charge on each capacitor.
 View Solution
View SolutionFind charge on each capacitor
 View Solution
View SolutionFind the potential difference and charge on each capacitor.
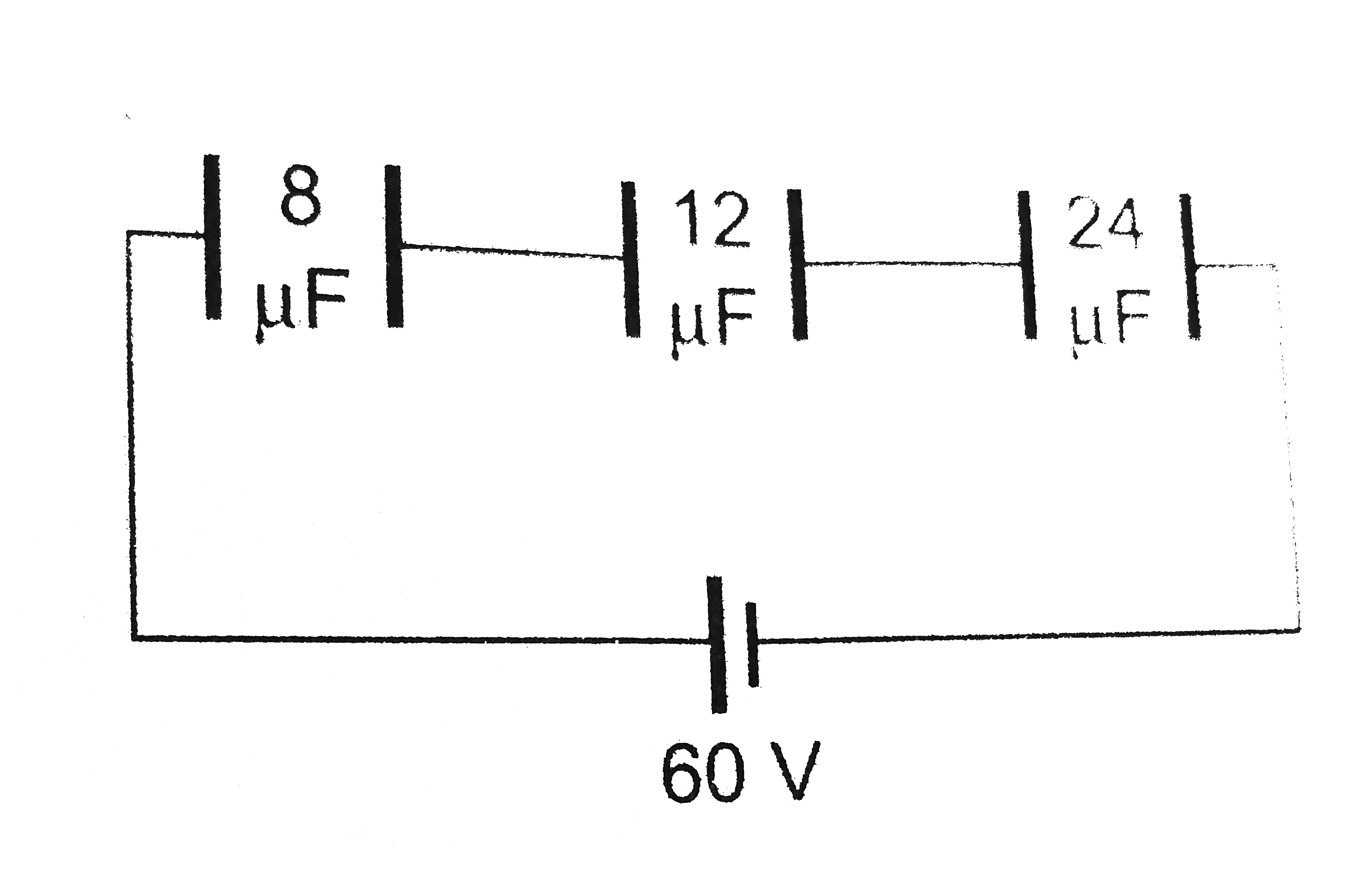 View Solution
View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionTwo capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.View Solution