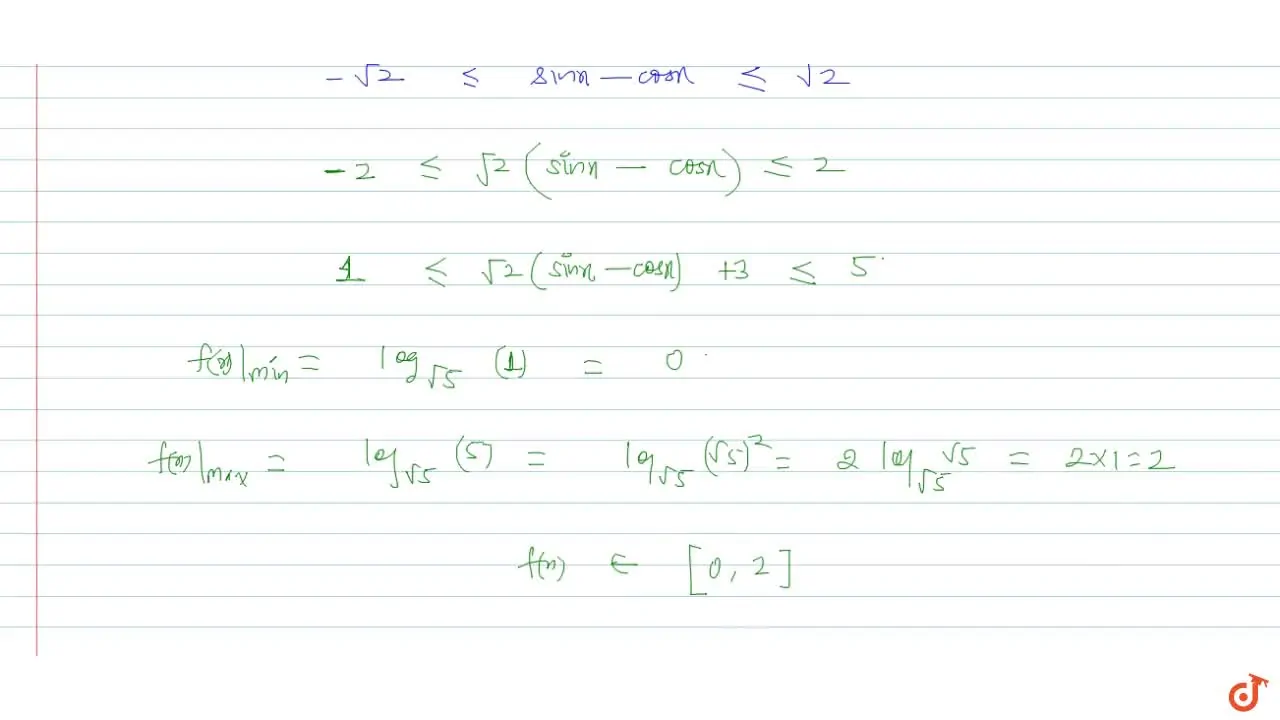The range of $f (x) = {log}_{\sqrt{5}} (\sqrt{2} (sin x - cos x) + 3)$ is

A

$[0, 1]$

B

$[0, 2]$

C

$[0, \frac{3}{2}]$

D

$[1, 2]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

NA

|

Updated on:21/07/2023

Class 12 MATHS RELATIONS AND FUNCTIONS

Topper's Solved these Questions

BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - INTEGER_TYPE
21videos
RELATION, FUNCTION & ITF
BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MCQ_TYPE
31videos
RELATION, FUNCTION & ITF
BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN
5videos
RELATION, FUNCTION & ITF
BOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4videos
NUMBER THEORY
BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3videos
SEQUENCE & SERIES

Similar Questions

Knowledge Check

Question 1 - Select One
The range of ${log}_{\sqrt{5}} [\sqrt{2} (sin x - cos x) + 3]$ is :
A[0,2]
B[1,2]
C[0,3]
D[1,3]
Question 2 - Select One
Range of $f (x) = {log}_{\sqrt{10}} (\sqrt{5} (2 sin x + cos x) + 5)$ is :
A[0,1]
B[0,3]
C $(- \infty, \frac{1}{3}]$
DNone of these
Question 3 - Select One
The range of $f (x) = cos x - sin x$ is
A $[- 1, 1]$
B $(- 1, 2)$
C $[- \frac{π}{2}, \frac{π}{2}]$
D $[- \sqrt{2}, \sqrt{2}]$

RESONANCE-RELATION, FUNCTION & ITF-SCQ_TYPE

Home
Ask Doubt
Profile