Let g(x)=1+x−[x]andf(x)={−1,x<00,x=0f,x>0 . Then for all x,f(g(x)) is equal to (where [.] represents the greatest integer function). x (b) 1 (c) f(x) (d) g(x)
A
x
B
1
C
f(x)
D
g(x)
Video Solution
Text Solution
The correct Answer is:B
NA
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - INTEGER_TYPE21videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MCQ_TYPE31videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN5videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)4videos
NUMBER THEORY
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Let g(x)=1+x−[x]andf(x)=⎧⎪⎨⎪⎩−1,x<00,x=01,x>0, then for all x,f[g(x)] is equal to
A0B1CxDf(x) - Question 2 - Select One
Let g(x)=1+x-[x] and
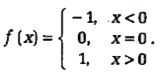Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x) - Question 3 - Select One
If f(x)=Sgn x and g(x)=1+x-[x], then for all x, f(g(x)) is equal to :
A0B1CxDf(x)
Let g(x)=1+x−[x]andf(x)=−1 if x<0=0 if x>0, then f∣g(x)]=1x>0
View SolutionLet f(x)=∣∣∣(x+12)[x]∣∣∣,when −2≤x≤2∣. where [.] represents greatest integer function. Then
View SolutionLet g(x) = 1 + x – [x] and f(x)=⎧⎪⎨⎪⎩−1ifx<00ifx=01ifx>0 then Aax,fog(x) equals
(where [ * ] represents greatest integer function).View SolutionLet f(x)=|x|andg(x)=[x], (where [.] denotes the greatest integer function) Then, (fog)'(−1) is
View SolutionIf f(x)={1−|x|1+xx≠−11x=−1, then f([2x]) is (where [*] represent greatest integer function)
View Solution