A man observe that was he has climbed up $\frac{1}{3}$ of the length of an inclined ladder ,placed against a wall the angular depression of an object on the floor is $α$ and that after he reached the top of the ledder , the angular depression $β$ If the inclintaion of the ladder to the is $θ$ then prove that cot $θ = \frac{3 cot β - cot α}{2}$

Video Solution

Text Solution

Verified by Experts

Let AB be the ladder and the object be ay point O.

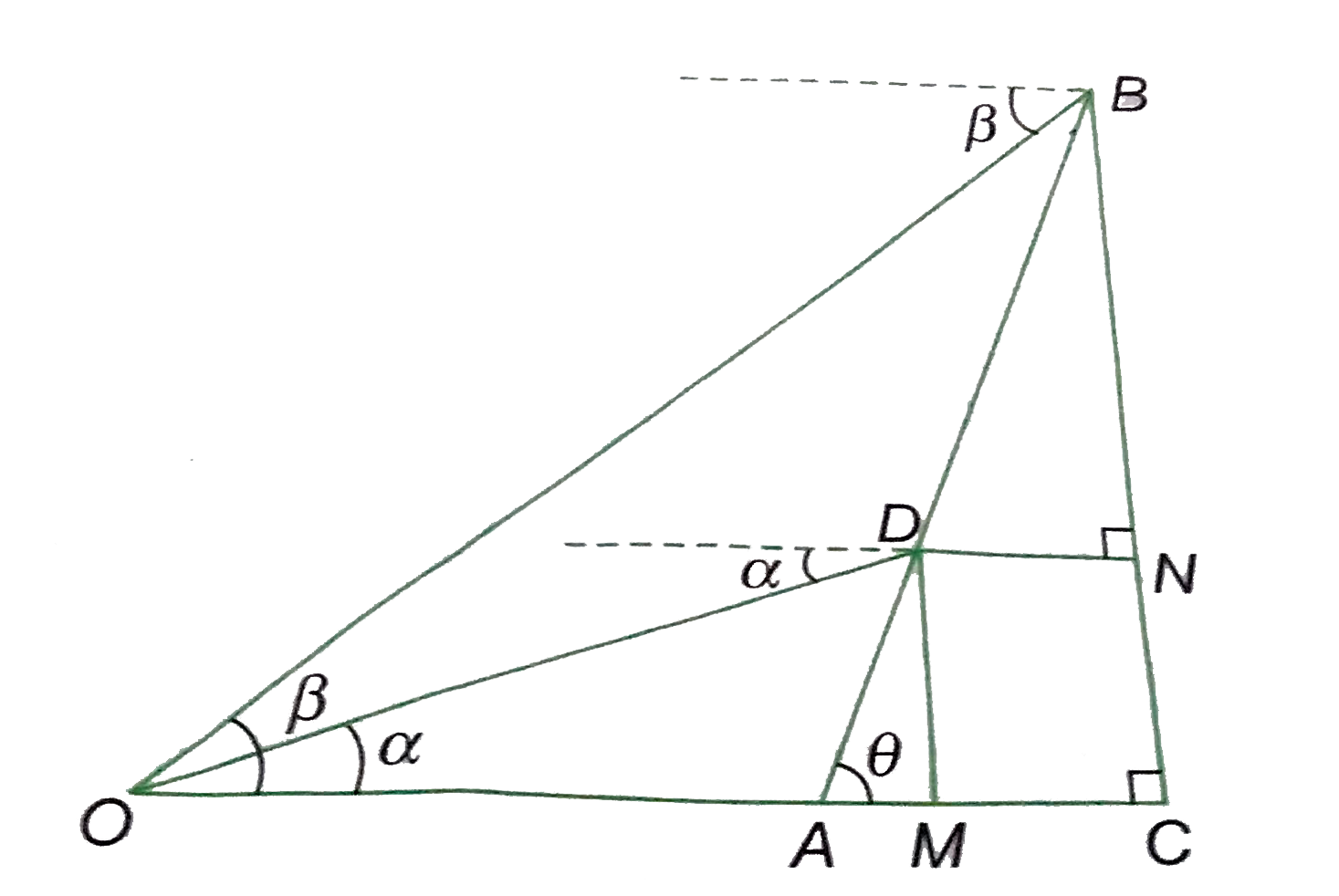
Also ,let l length of the ladder and the man be at point D intitially .
In triangle AMD, DM = AD sin $θ = \frac{1}{3} l sin θ$
In triangle ACB,BC $= l sin θ$
In triangle OMD, OM $= D M cot α = \frac{1}{3} l sin θ cot α$
In triangle OCB, OC = BC cot $β = l sin θ cot β$
Now ,MC = OC - OM = l sin $θ cot β - \frac{1}{3} l sin θ cot α ... . . (1)$
Also , MC = DN $= \frac{2}{3} l cos θ$ (From triangle BND)
$∴ l sin θ cot β - \frac{1}{3} l sin θ α = \frac{2}{3} l cos θ$
$\Rightarrow (3 cot β - cot α) sin θ = 2 cos θ$
$\Rightarrow cot θ = \frac{3 cot β - cot α}{2}$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A tower AB leans towards west making an angle $α$ with the vertical . The anlgular elevation of B , the topmost point of the tower is $β$ as obsreved from a point C due east of A at distance d from A.If the angular elevation of B from a pont D at a distance 2d due east of C is $γ$ , then prove that 2 tan $α$ = cot $γ$ -cot $β$
A $2 tan α = 2 cot β - cot γ$
B $2 tan α = 3 cot β - cot γ$
C $tan α = cot β - cot γ$
DNone of these
Question 2 - Select One
A ladder rests against a wall at an acute angle $α$ to the horizontal. Its foot is pulled away form the wall through a distance 2 m, so that it slides a distance 3 m down the wall making an acute angle $β$ with the horizontal , then the value of $tan (\frac{α + β}{2})$ is
A $\frac{3}{2}$
B $\frac{2}{3}$
C $\frac{4}{9}$
D $\frac{9}{4}$

CENGAGE-HIGHT AND DISTANCE -JEE Previous Year

Home
Ask Doubt
Profile