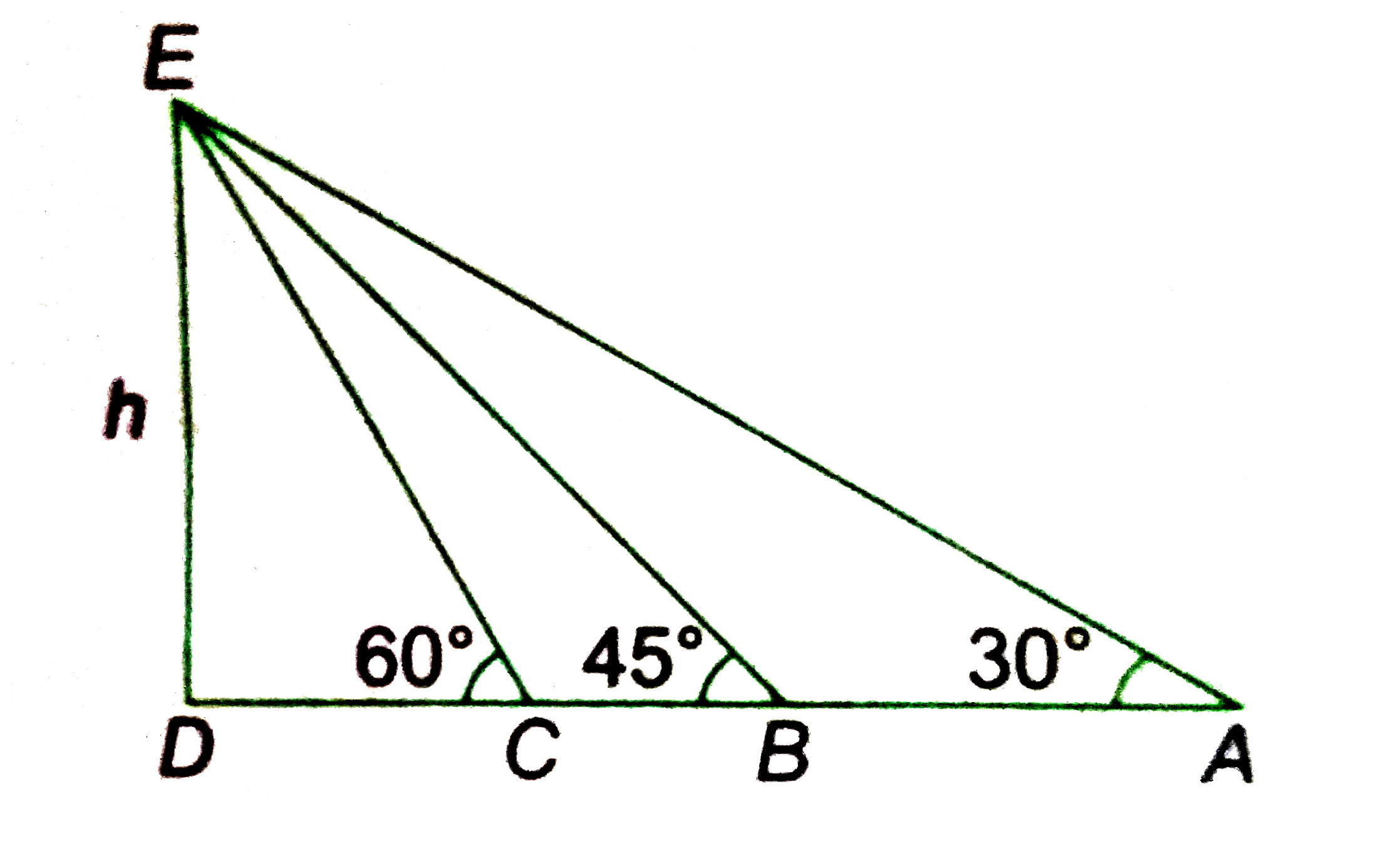
If the angles of elevation of the top of a tower from three collinea

If the angles of elevation of the top of tower from three collinear points $A$ , $B$ and $C$ , on a line leading to the foot of the tower, are $30^{\circ}$ , $45^{\circ}$ and $60^{\circ}$ respectively, then the ratio , $A B : B C$ is
A $\sqrt{3} : 1$
B $\sqrt{3} : \sqrt{2}$
C $1 : \sqrt{3}$
D $2 : 3$
Angles of elevation of the top of a tower from three point (collinear) A, B and C on a road leading to the food of the tower are $30^{\circ}, 45^{\circ}$ and $60^{\circ}$ respectively. The ratio of AB to BC is
A $\sqrt{3} : 1$
B $\sqrt{3} : 2$
C $1 : 2$
D $2 : \sqrt{3}$
The angle of elevation of the top of a TV tower from three points A,B and C in a straight line through the foot of the tower are $α, 2 α$ and $3 α$ , respectively. If $A B - α$ , then height of the tower is
A $a tan α$
B $a sin α$
C $a sin 2 α$
D $a sin 3 α$

If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are $30^{0}$ , $45^{0}$ and $60^{0}$ respectively, then the ratio, AB : BC, is : (1) $\sqrt{3} : 1$ (2) $\sqrt{3} : \sqrt{2}$ (3) $1 : \sqrt{3}$ (4) $2 : 3$