SO3(g)⇔SO2(g)+12O2(g)
If observed vapour density of mixture at equilibrium is 35 then find out value of α
0.28
0.38
0.48
0.58
The correct Answer is:A
To solve the problem, we need to find the value of alpha (α) in the equilibrium reaction:
SO3(g)⇌SO2(g)+12O2(g)
Given that the observed vapor density (d) of the mixture at equilibrium is 35, we can follow these steps:
Step 1: Calculate the molar mass of SO3
The molar mass of SO3 can be calculated as follows:
- Molar mass of S = 32 g/mol
- Molar mass of O = 16 g/mol
Thus, the molar mass of SO3 is:
Molar mass of SO3=32+(16×3)=32+48=80g/mol
Step 2: Calculate the vapor density (D) of SO3
The vapor density (D) is defined as half of the molar mass:
D=Molar mass of SO32=802=40
Step 3: Determine the number of moles of products
From the reaction, we can see:
- 1 mole of SO2
- 0.5 moles of O2
Thus, the total number of moles of products (n) is:
n=1+12=1.5
Step 4: Use the formula for alpha (α)
The formula to calculate alpha is given by:
α=D−d(n−1)⋅d
Substituting the values we have:
- D = 40
- d = 35
- n = 1.5
We can now substitute these values into the formula:
α=40−35(1.5−1)⋅35
Step 5: Calculate α
Now, we calculate the numerator and denominator:
- Numerator: 40−35=5
- Denominator: (1.5−1)⋅35=0.5⋅35=17.5
Thus,
α=517.5
Calculating this gives:
α=0.2857≈0.28
Final Answer
The value of alpha (α) is approximately 0.28.
---
The molar mass of SO3 can be calculated as follows:
- Molar mass of S = 32 g/mol
- Molar mass of O = 16 g/mol
Molar mass of SO3=32+(16×3)=32+48=80g/mol
The vapor density (D) is defined as half of the molar mass:
D=Molar mass of SO32=802=40
From the reaction, we can see:
- 1 mole of SO2
- 0.5 moles of O2
n=1+12=1.5
The formula to calculate alpha is given by:
α=D−d(n−1)⋅d
- D = 40
- d = 35
- n = 1.5
α=40−35(1.5−1)⋅35
Now, we calculate the numerator and denominator:
- Numerator: 40−35=5
- Denominator: (1.5−1)⋅35=0.5⋅35=17.5
α=517.5
α=0.2857≈0.28
The value of alpha (α) is approximately 0.28.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-1)
Explore 28 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-2)
Explore 23 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-1 (Part-1)
Explore 38 Videos
- CHEMICAL BONDINGBook:RESONANCEChapter:CHEMICAL BONDINGExercise:Inorganic chemistry (Chemistry Bonding)
Explore 49 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Book:RESONANCEChapter:D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Exercise:Match the column
Explore 1 Video
Similar Questions
At 627∘C and 1 atm pressure, SO3 undergoes partial dissociation into SO2 and O2
SO3⇔SO2+12O2
if the observed density of the equilibrium mixture is 0.925 g/L, calculate degree of dissociation of SO3.
View SolutionAt 627∘C and 1 atm SO3 is partially dissociated into SO2 and O2 by the reaction
SO3(g)⇔SO2(g)+12O2(g)
The density of the equilibrium mixture is 0.925gL−1. What is the degree of dissociation?
View Solution
Knowledge Check
At 727∘C and 1.2atm of total equilibrium pressure, SO3 is partially dissociated into SO2 and O2 as:
SO3(g)⇔SO2(g)+12O2(g)
The density of equilibrium mixture is 0.9g/L. The degree of dissociation is:, [UseR=0.08atmLmol−1K−1]A13B23C14D14Before equilibrium is set-up the chemical reaction N2O4(g)⇔2NO2(g), vapour density d of the gaseous mixture was measured. If D is the theoretica value of vapour density, variation of α with D/d is given by the graph below. What is value D/d at point A ?
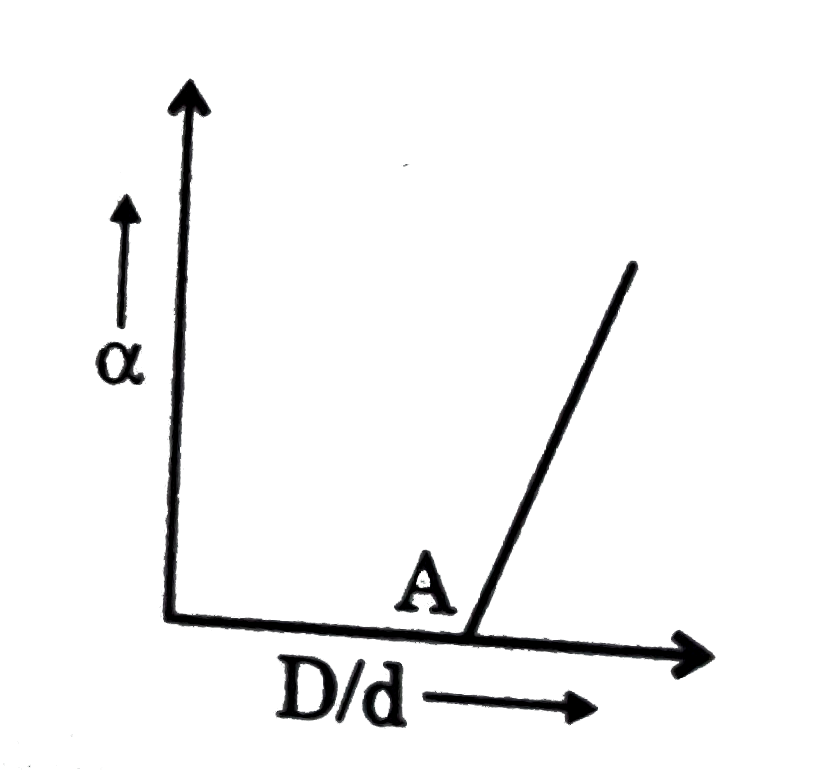 A1B0.5C1D1.5
A1B0.5C1D1.5For the reaction N2O(g)⇔2NO2(g).ΔH=57.49kJ/ mole, the vapour density of equilibrium mixture ……………………….. with increase of temperature.
AincreasesBdecreasesCRemain sameDcan not be predicted
At 627∘C and 1 atm SO3 is partially dissociated into SO2 and O2 by the reaction
SO3(g)⇔SO2(g)+1/2O2(g)
The density of the equilibrium mixture is 0.925gL−1. What is the degree of dissociation?
View SolutionSO3(g)+CO(g)⇔SO2(g)+CO2(g)
Which of the following activity can reduce the equilibrium concentration of CO to half?
View SolutionCaCO3(s)⇔CaO(s)+CO2(g)
CO2(g)⇔CO(g)+12O2(g)
For above simultaneous equilibrium if CO2 is added from out side at equilibrium then:
View SolutionFor the equlibrium SO3(g)⇔SO2(g)+12O(2)(g) the molar mass at equlibrium was observed to be 60. then the degree of dissociation of SO3 would be
View SolutionConsider the equilibrium
SO3(g)⇔SO2(g)+12O2(g) KC=1
What should be the initial concentration so that at equilibrium [SO3]=[O2]
View Solution

