The effect of temperature on equilibrium constant is expressed as(T2>T1)
logK2/K1=−ΔH2.303[1T2−1T1]. For endothermic, false statement is
[1T2−1T1]=positive
ΔH=positive
logK2>logK1
K2>K1
The correct Answer is:A
log K_(2)//logK1=−ΔH2.303[1T2−1T1]⇒ΔH=positive
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-1)
Explore 28 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-2)
Explore 23 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCEChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-1 (Part-1)
Explore 38 Videos
- CHEMICAL BONDINGBook:RESONANCEChapter:CHEMICAL BONDINGExercise:Inorganic chemistry (Chemistry Bonding)
Explore 49 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Book:RESONANCEChapter:D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Exercise:Match the column
Explore 1 Video
Similar Questions
Variation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Select the correct statement :
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
For an isomerization X(g)⇔Y(g) the temperature dependency of equilibrium cohnstant is given by :
lnK=2−1000T
The value of ΔrS∘ at 300K is :
View Solution
Knowledge Check
The efffect of temperature on equilibrium consatant is expressed as,
log[K2K1]=−ΔH2.303[1T2−1T1],(T2>T1)
For endothermic reaction false statement is :
(d) K2K1.A(T2>T1) =positiveBΔH=positiveClogK2>logK1DK2K1.Effect of temperature of equilibrium constant is given by logK2−logK1=−ΔH2.303R[1T2−1T1]( where T2>T1). Then for a endothermic reaction the false statement is
A[1T2−1T1]= positiveBlogK2>logK1CΔH= positiveDK2>K1For a reversible reaction aA+bB⇔cC+dD, the variation of K with temperature is given by log K2K1=−ΔH∘2.303R[1T2−1T1] then,
AK2>K1ifT2>T1 for an endothermic changeBK2<K1ifT2>T1 for an endothermic changeCK2>K1ifT2>T1 for an endothermic changeDK2>K1ifT2>T1 for an endothermic change
Each question contains STATEMENT-1 (Assertion) and STATEMENT-2( Reason).
Examine the statements carefully and mark the correct answer according to the instruction given below:
STATEMENT-1: The equilibrium constant of the exothermic reaction at high temperature decreases.
STATEMENT-2: Since In K2K1=ΔH∘R[1T1−1T2] and for exothermic reaction ,
ΔH∘=-ve and thereby, K2K1<1
View SolutionFor a reversible reaction αA+βB⇔.cC+.dD,the variation of K with temperature is given by logK2K1=−ΔH∘2.303R[1T2−1T1]then,
View SolutionFor a reaction, aA+bB⇔cC+dD, the reaction quotient Q=[C]c0[D]d0[A]a0[B]b0, where [A]0, [B]0, [C]0, [D]0 are initial concentrations. Also Kc=[C]c[D]d[A]a[B]b where [A], [B], [C], [D] are equilibrium concentrations. The reaction proceeds in forward direction if Q<Kc and in backward direction if Q>Kc. The variation of Kc with temperature is given by: 2303log(KC2)KC1=ΔHR[T2−T1T1T2].
For gaseous phase reactions Kp=Kc(RT)Δn where Δn= moles of gaseous products − moles of gaseous reactants. Also −ΔG∘=2.303RTlog10Kc.
(B) The moisture content of a gas is often expressed as dew point, the temperature at which if gas is cooled becomes saturted with vapour pressure of water at that temperture. Dew point of H2O is 43∘C having vapour pressure 0.07torr.
CaCl2⋅2H2O(s)⇔CaCl2(s)+2H2O(g),
The equilibrium constant should not be more than..... (atm)2 if CaCl2 is to be used as desiccant.
View SolutionWhen the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
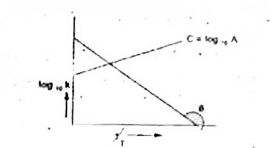
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate of certain reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If k is the rate constant at 300K then rate constant at 310K will be equal to
View SolutionFor a reaction, aA+bB⇔cC+dD, the reaction quotient Q=[C]c0[D]d0[A]a0[B]b0, where [A]0, [B]0, [C]0, [D]0 are initial concentrations. Also Kc=[C]c[D]d[A]a[B]b where [A], [B], [C], [D] are equilibrium concentrations. The reaction proceeds in forward direction if Q<Kc and in backward direction if Q>Kc. The variation of Kc with temperature is given by: 2303log(KC2)KC1=ΔHR[T2−T1T1T2].
For gaseous phase reactions Kp=Kc(RT)Δn where Δn= moles of gaseous products − moles of gaseous reactants. Also −ΔG∘=2.303RTlog10Kc.
Which relation is correct?
View Solution

