A fountain jet situated at a height of 11.25 m above the ground projects water droplets in all directions with velocity of 20 m/s. Calculate the maximum distance (in m) on ground reached by any water droplet
50 m
100 m
75 m
25 m
The correct Answer is:A
To solve the problem of calculating the maximum distance on the ground reached by any water droplet projected from a fountain jet situated at a height of 11.25 m with an initial velocity of 20 m/s, we can follow these steps:
Step 1: Understand the Problem
The fountain is at a height of 11.25 m and projects water droplets at a speed of 20 m/s in all directions. We need to find the maximum horizontal distance (range) that any droplet can reach when projected at an angle.
Step 2: Break Down the Motion
The motion of the water droplet can be analyzed in two components:
1. Vertical motion (affected by gravity)
2. Horizontal motion (constant velocity)
Step 3: Determine the Time of Flight
The vertical motion can be described using the kinematic equation:
y=vyt−12gt2
Where:
- y is the vertical displacement (which will be -11.25 m, as it falls down)
- vy is the initial vertical velocity component, which can be expressed as vsinθ
- g is the acceleration due to gravity (approximately 9.81m/s2)
- t is the time of flight
Setting up the equation:
−11.25=(20sinθ)t−12(9.81)t2
Step 4: Solve for Time
Rearranging gives us a quadratic equation in terms of t:
12(9.81)t2−(20sinθ)t−11.25=0
Using the quadratic formula:
t=−b±√b2−4ac2a
Where:
- a=12(9.81)
- b=−20sinθ
- c=−11.25
Step 5: Find the Horizontal Distance
The horizontal distance x can be expressed as:
x=vxt
Where vx=vcosθ and v=20m/s.
Step 6: Maximize the Range
To find the maximum distance, we need to maximize x. The maximum range occurs when the angle θ is 45 degrees (for projectile motion). Thus, we can substitute sin(45∘)=cos(45∘)=1√2.
Step 7: Calculate Time of Flight for θ=45∘
Substituting sin(45∘) into the time of flight equation:
−11.25=(20⋅1√2)t−12(9.81)t2
Step 8: Solve for Time
This will yield a specific time t that can be substituted back into the horizontal distance formula.
Step 9: Calculate the Maximum Distance
Substituting the time back into the horizontal distance equation will yield the maximum distance x.
Final Calculation
After solving the equations, we find that the maximum horizontal distance x is approximately 50 m.
Summary
The maximum distance on the ground reached by any water droplet is 50 m.
---
The fountain is at a height of 11.25 m and projects water droplets at a speed of 20 m/s in all directions. We need to find the maximum horizontal distance (range) that any droplet can reach when projected at an angle.
The motion of the water droplet can be analyzed in two components:
1. Vertical motion (affected by gravity)
2. Horizontal motion (constant velocity)
The vertical motion can be described using the kinematic equation:
y=vyt−12gt2
Where:
- y is the vertical displacement (which will be -11.25 m, as it falls down)
- vy is the initial vertical velocity component, which can be expressed as vsinθ
- g is the acceleration due to gravity (approximately 9.81m/s2)
- t is the time of flight
−11.25=(20sinθ)t−12(9.81)t2
Rearranging gives us a quadratic equation in terms of t:
12(9.81)t2−(20sinθ)t−11.25=0
t=−b±√b2−4ac2a
Where:
- a=12(9.81)
- b=−20sinθ
- c=−11.25
The horizontal distance x can be expressed as:
x=vxt
Where vx=vcosθ and v=20m/s.
To find the maximum distance, we need to maximize x. The maximum range occurs when the angle θ is 45 degrees (for projectile motion). Thus, we can substitute sin(45∘)=cos(45∘)=1√2.
Substituting sin(45∘) into the time of flight equation:
−11.25=(20⋅1√2)t−12(9.81)t2
This will yield a specific time t that can be substituted back into the horizontal distance formula.
Substituting the time back into the horizontal distance equation will yield the maximum distance x.
After solving the equations, we find that the maximum horizontal distance x is approximately 50 m.
The maximum distance on the ground reached by any water droplet is 50 m.
Topper's Solved these Questions
Similar Questions
A stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View Solution
Knowledge Check
An aeroplane is flying at a height of 1960 m in horizontal direction with a velocity of 360 km/hr. When it is vertically above the point. A on the ground, it drops a bomb. The bomb strikes a point B on the ground, then the time taken by the bomb to reach the ground is-
A20√2secB20secC10√2 secD10 secA body is projected horizontally from a height of 20m. It reaches the ground at a horizontally distance of 40m. The speed of practicle when it hits the ground is
A10m/sB10√m/sC20m/sD20√2m/sWater is flowing through a horizontal pipe fixed at a height of 2 m above the ground as shown in Fig. 5.90. water strikes ground at a distance of 3m from the pipe. The speed of water as it leaves the pipe is:
 A47m/sB4.7m/sC9.4m/sD4.9m/s
A47m/sB4.7m/sC9.4m/sD4.9m/s
A body moving on the ground with a velocity of 15m/s comes to rest after covering a distance of 25m If acceleration due to gravity is 10m/s2 Calculate the coefficient of friction between the ground and the body .
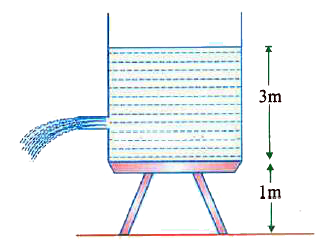
View SolutionWater is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View SolutionA girl in a swing is 2.5 m above ground at the maximum height and at 1.5 m above the ground at the lowest point. Her maximum velocity in the swing is (g=10ms−2)
View SolutionA girl in a swing is 2.5 m above ground at the maximum height and at 1.5 m above the ground at the lowest point, Her maximum velocity in the swing is (g=10ms−2)
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View Solution
