A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
8 cm
2 cm
40 cm
4 cm
The correct Answer is:A
→v=αˆi+βtˆj
d→vdt=βˆj⇒atotal=β
|→v|=√α2+β2t2
at=dvdt=2β2t2√α2+β2t2
(at)=β2(α√3β)√α2+β2α23β2=β2(α√3β)2α
at=√32β
aNormal=√a2total−a21=√β2−3β24=β2
Topper's Solved these Questions
Similar Questions
The product of the numbers 5623 and 6 in the scale of eight is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View Solution
Knowledge Check
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2gA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2
A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
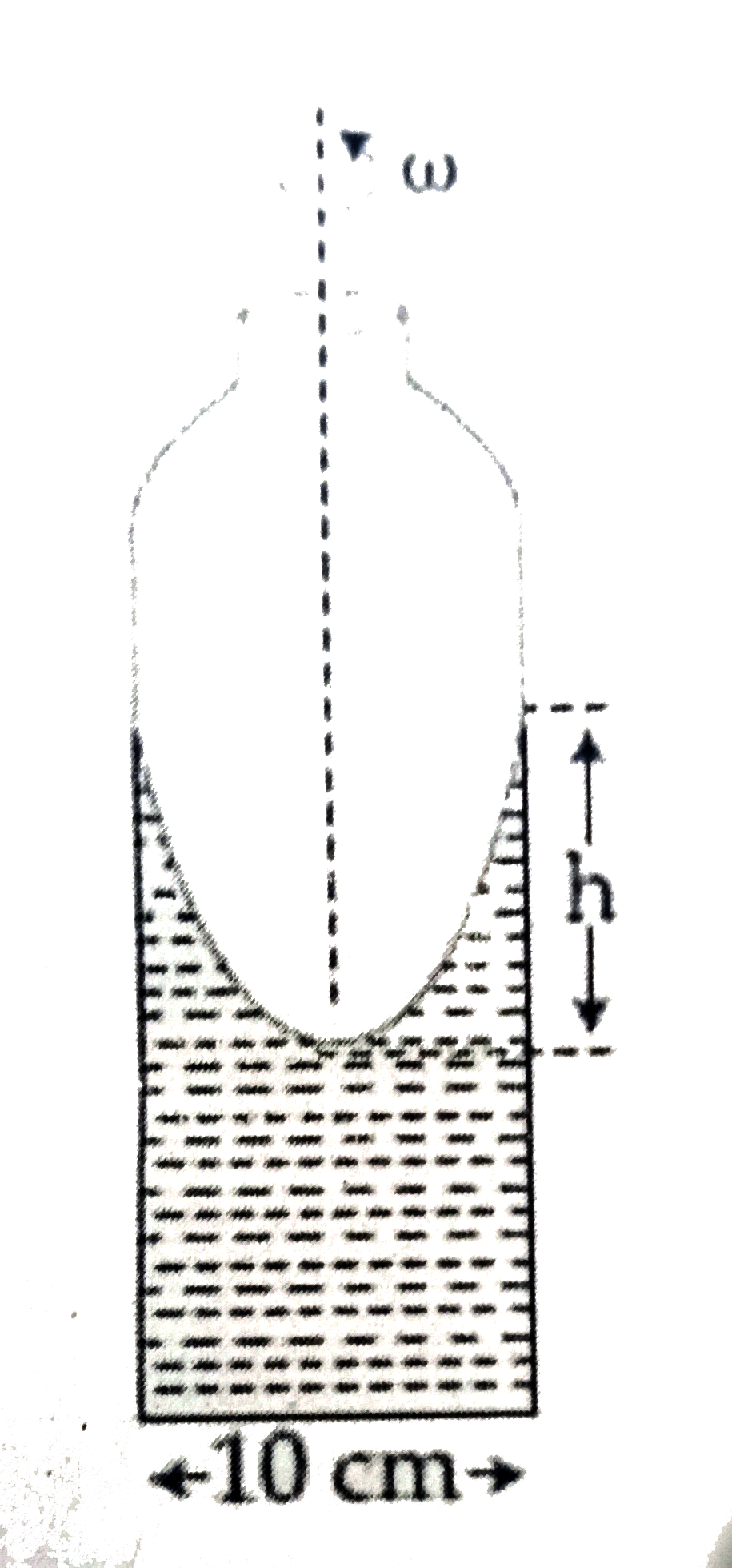
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA liquid is kept in a cylindrical jar, which is rotated about the cylindrical axis. The liquid rises at its sides. The radius of the jar is r and speed of rotation is Ω the difference in height at the centre and the sides of the jar is
View SolutionA liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
View SolutionA long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
View Solution
