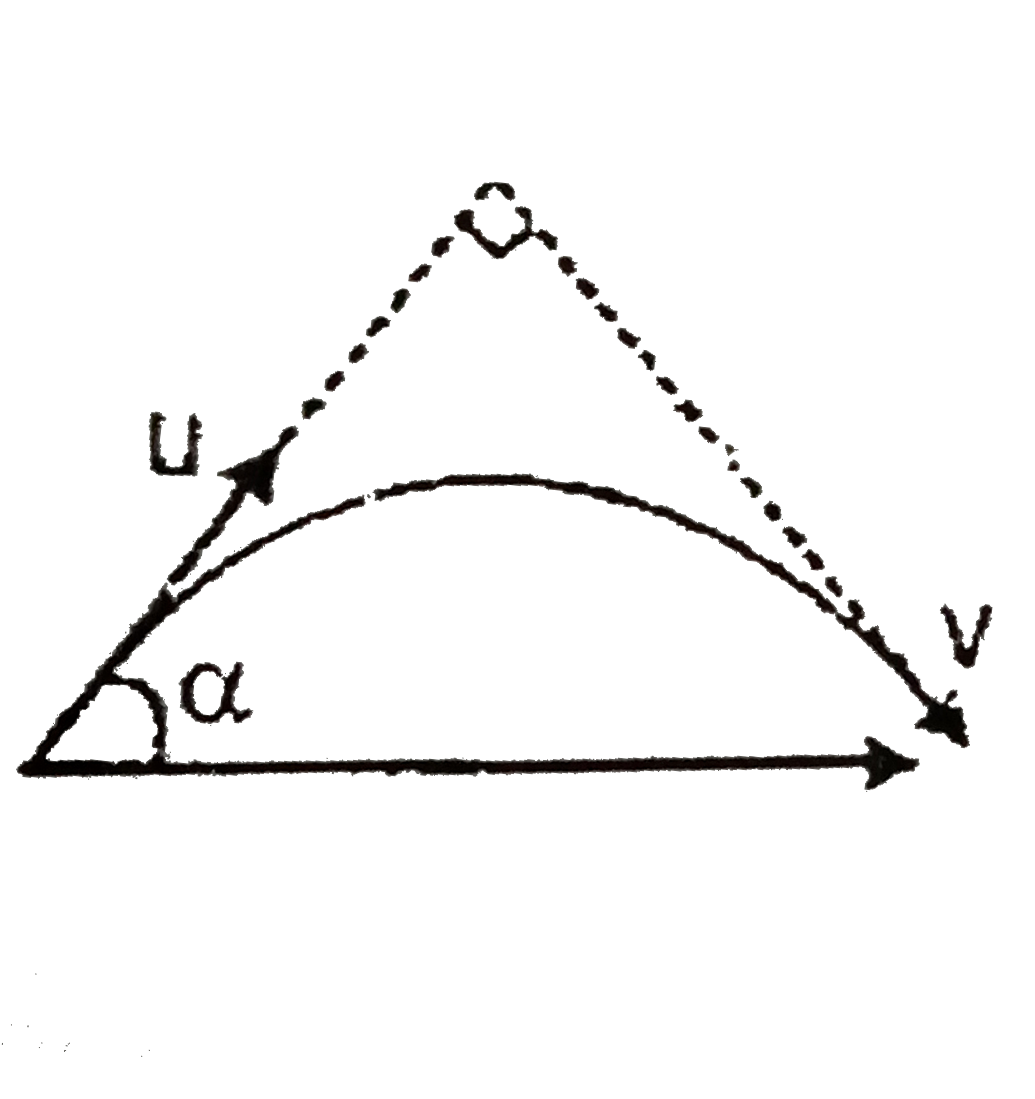
A particle is projected from a point O with a velocity u at an angle $α$ (upwards) to the horizontal. At a certain point P it moves at right angles to its initial direction. It follows that:

A

OP makes an angle ${tan}^{- 1} (u / 2 g)$ to the horizontal

B

the distance of P from O is $u / (2 g sin α)$ .

C

the time of flight from O to P is $u / (g sin α)$

D

the velocity of the particle at P is u cot $α$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C, D

Taking initial and final velocity on x and y axis.
0 = u - g sin $α t$
$t = \frac{u}{g {sin}^{2}}$
$x = u [\frac{u}{g {sin}^{2}}] - \frac{1}{2} (g sin α) {[\frac{u}{(g {sin}^{2})}]}^{2} =$
$\frac{u^{2}}{2 g sin α}$
$y = \frac{1}{2} g cos a {[\frac{u}{g sin α}]}^{2} = \frac{u^{2}}{2 g} (\frac{cos α}{{sin}^{2} α})$

OP = $\sqrt{x^{2} + y^{2}} = \frac{u^{2}}{2 g sin α}$
$tan ϕ = \frac{y}{x} = \frac{cos α x sin α}{{sin}^{2} α} = cot α$
$v = 0 + g cos a [\frac{u}{g sin α}] = u cot α$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected from a point P with a velocity v at an angle $θ$ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
AVelocity of particle at Q is $v sin θ$
BVelocity of particle at Q is $v cot θ$
CTime of flight from P to Q is $(v / g) cos e c θ$
DTime of flight from P to Q is $(v / g) sec θ$
Question 2 - Select One
A particle is project d from point A with velocity u at an angle $α$ with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
A $u tan α$
B $u cot α$
C $u cos α$
D $u cos e c α$
Question 3 - Select One
A particle is projected with initial velocity u making an angle $α$ with the horizontal, its time of flight will be given by
A $\frac{2 u sin α}{g}$
B $\frac{2 u^{2} sin α}{g}$
C $\frac{u sin α}{g}$
D $\frac{u^{2} sin α}{g}$

VIBRANT-REVIEW TEST-PART - II : PHYSICS

Home
Ask Doubt
Profile