While solving a physics problem you perform a series of algebraic manipulations that lead to a mathematical expression for distance. If F = Force, a = acceleration, v = velocity, m = mass, t = time, and N = normal force, use dimensional analysis to find which of the following expressions could be INCORRECT for distance.
vtNF
v22a
mvaNt
ma−2t2N
The correct Answer is:D
[ma−2t2N]=[L−3T8]
Topper's Solved these Questions
Similar Questions
V - velocity, T - time, F - force is taken as fundamental quantities. Find dimension of mass [M].
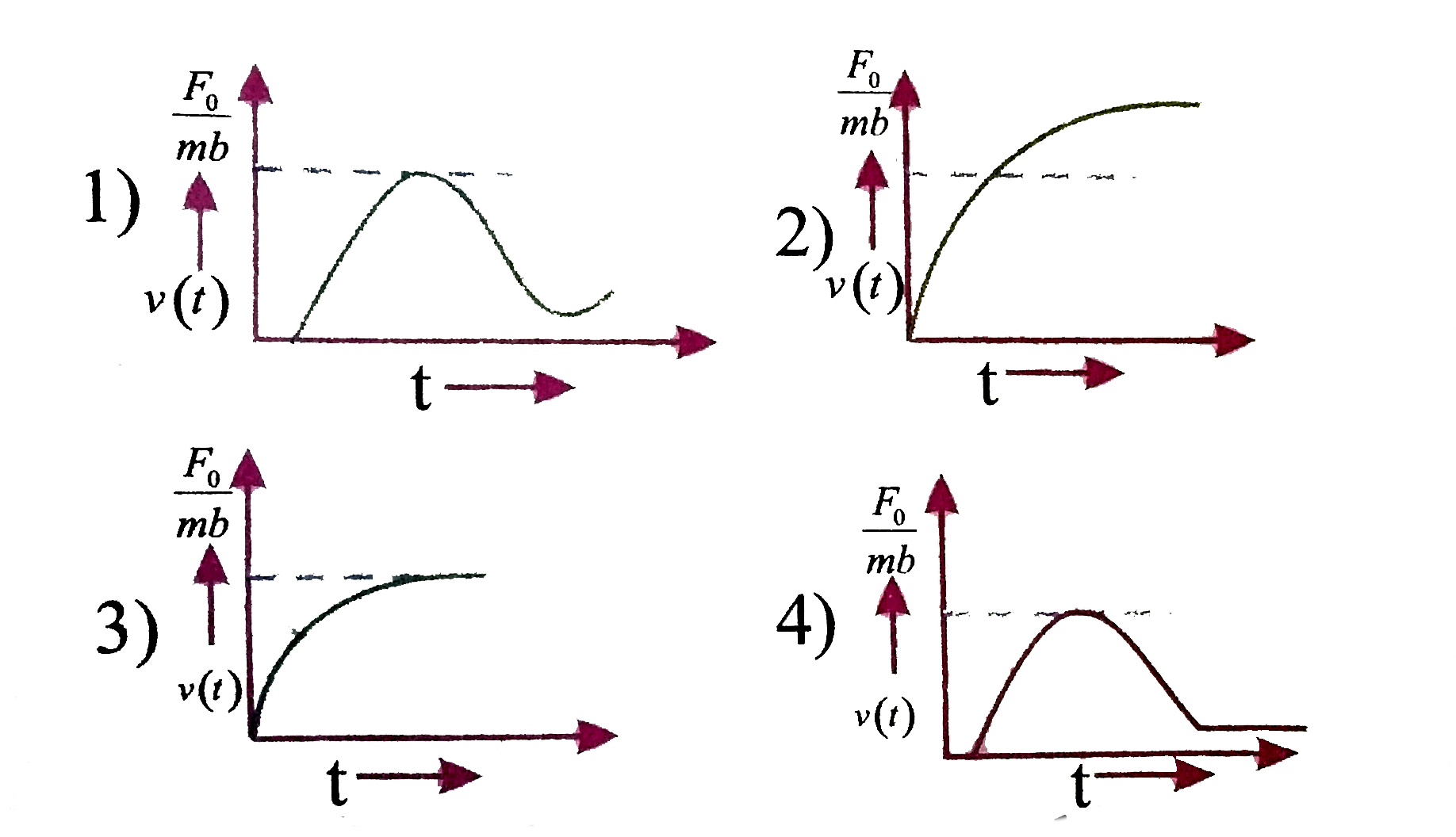
View SolutionA particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
View Solution
Knowledge Check
Which of the following cannot be the group of fundamental quantities.
(Here M is mass, L is length, T is time, F is force, A is acceleration, V is velocity)A(M,L,V)B(F,L,T)C(M,L,T)D(A,V,L)Test if the following equation is dimensionally correct: h=(sScosθrpg) where h= height, S= surface tension, p= density, r=radius, and g= acceleration due to gravity.
As=12at2Bv=√T/mCt=2hgDa=v2rThe formula W=(F+2Ma)vn, where W is the work done, F is the force, M is the mass, a is the acceleration and v is the velocity can be made dimensionally correct for
An=0Bn=1Cn=−1Dno value of n
A particle of mass m is at rest at the origin at time t=0. It is subjected to a force F(t)=F0e−bt in the X - direction. Its speed V(t) is depicted by which of the following curves.

View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :
View Solution

