The radial distribution functions $[P (r)]$ is used to determine the most probable radius, which is used to find the electron in a given orbital $\frac{d P (r)}{d r}$ for $1 s$ -orbital of hydrogen like atom having atomic number $Z$ , is $\frac{d P}{d r} = \frac{4 Z^{3}}{a_{0}^{3}} (2 r - \frac{2 Z r^{2}}{a_{0}}) e^{- 2 Z r / a_{0}}$ :

At the point maximum value of radial distribution function $\frac{d P (r)}{d r} = 0$ , one antinode is present

Most probable radius of $L i^{2 +}$ is $\frac{a_{0}}{3}$ pm

Most probable radius of $H e^{+}$ is $\frac{a_{0}}{2}$ pm

Most probable radius of hydrogen atom is $a_{0}$ pm

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

At the point of maximum value of RDF
$\frac{d P}{d r} = 0$
$(2 r - \frac{2 Z r^{2}}{a_{0}}) = 0, r = \frac{a_{0}}{Z}$
where $Z = 3$ for $L i^{2 +}$ and $Z = 2$ for the $H e^{+}, Z = 1$ for hydrogen.

Updated on:21/07/2023

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The plots of radial distribution function for various orbitals of hydrogen atom against 'r' are given below

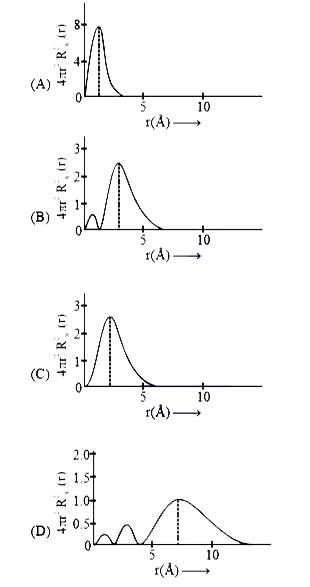
The correct plot for 3s orbital is :
A(B)
B(A)
C(D)
D $(C)$
Question 2 - Select One
The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
Psi_(2s) = ((Z)/(2a_(0)))^(½) (1-(Zr)/(a_(0)))e^(-(Zr)/(a_(0)))
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

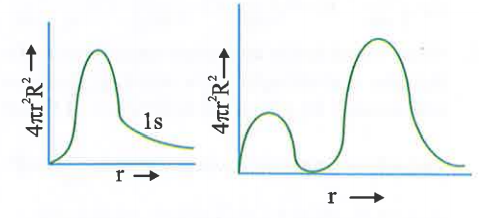
Answer the following questions:
The following graph is plotted for ns-orbitals

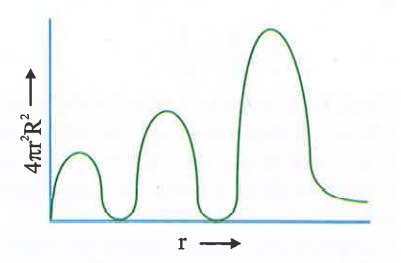
The value of 'n' will be:
A1
B2
C3
D4
Question 3 - Select One
The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

Answer the following questions:
The value of radius 'r' for 2s atomic orbital of H-atom at which the radial node will exist may be given as:
A $r = 2 a_{0}$
B $r = \frac{a_{0}}{4}$
C $r = a_{0}$
D $r = \frac{a_{0}}{5}$

RESONANCE-NUCLEAR CHEMISTRY-PART-II SECTION-1

Home
Ask Doubt
Profile

The radial distribution functions [ P ( r ) ] is used to determine the most probable radius, which is used to find the electron in a given orbital d P ( r ) d r for 1 s -orbital of hydrogen like atom having atomic number Z , is d P d r = 4 Z 3 a 0 3 ( 2 r - 2 Z r 2 a 0 ) e - 2 Z r / a 0 :

The correct Answer is:A, B, C, D

At the point of maximum value of RDF d P d r = 0 ( 2 r - 2 Z r 2 a 0 ) = 0 , r = a 0 Z where Z = 3 for L i 2 + and Z = 2 for the H e + , Z = 1 for hydrogen.

Topper's Solved these Questions

Similar Questions

Knowledge Check

The plots of radial distribution function for various orbitals of hydrogen atom against 'r' are given below The correct plot for 3s orbital is :

RESONANCE-NUCLEAR CHEMISTRY-PART-II SECTION-1

At the point of maximum value of RDF
$\frac{d P}{d r} = 0$
$(2 r - \frac{2 Z r^{2}}{a_{0}}) = 0, r = \frac{a_{0}}{Z}$
where $Z = 3$ for $L i^{2 +}$ and $Z = 2$ for the $H e^{+}, Z = 1$ for hydrogen.

The plots of radial distribution function for various orbitals of hydrogen atom against 'r' are given below

The correct plot for 3s orbital is :