A steel wire of length 50√3cm is connected to an aluminium wire of length 60cm and stretched between two fixed supports. The tension produced is 104N, if the cross section area of each wire is 1mm2. If a transverse wave is set up in the wire, find the lowest frequency for which standing waves with node at the joint are produced . (density of aluminimum =2.6gm/cm3 and density of steel =7.8gm/cm3).
The correct Answer is:1000/3Hz
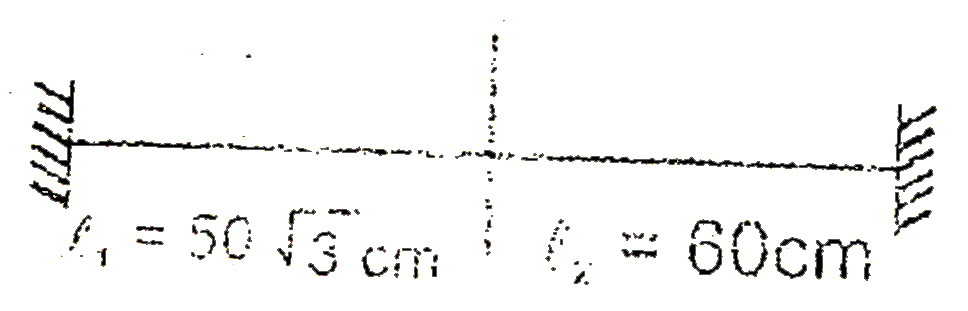
Steel , Aluminium
T=104
σ1=7.8gm/cm3,σ2=2.6gm/cm3
A1=A2=1mm2
V1=√Tσ1AT=
⎷1047.8×10−310−6×1×10−6
V1=(200√3)m/sec.
v2√Tσ2A2=√1042.6×10−3
=2×102m/sec.
for lowest freq.
f1=f2
n1V12L1=n2V22L2
n1×2002×√3×50√3=n2×2002×60×1
⇒[n1n2=(52)]
So lowest freq.
f2=n2V2L=2×2002×0.6=10003Hz
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 3 PART II
Explore 7 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 2 PART IV
Explore 9 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is .1.0mm2 and that of the aluminium wire is 3.0 mm 2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node ? The density of aluminium is 2.6gcm−3and that of steel is 7.8gcm−3

View SolutionFigure shows an aluminium wire of length 60cm joined to a steel wire of length 80cm and stretched between two fixed supports. The tension produced is 40N. The cross-sectional area of the steel wire is 1.0mm2 and that of the aluminimum wire is 3.0mm2 The minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node is 10P (in Hz) the find P. Given density of aluminimum is 2.6g/cm3 and that of steel is 7.8g/cm3.

View Solution
Knowledge Check
The tension produced in a sonometer wire is 60 N and the length between two bridges is 40 cm. The length of wire is 1 m and the mass of the wire is 2g. The speed of transverse waves produced in the wire is
A100 m/sB173.2 m/sC200 m/sD150 m/sAn aluminium wire and a steel wire of same cross-sectional of 10−2cm2 were connected together. A 10 kg block loaded on the compound wire as shown in figure. Waves are set up in the compound wire. The minimum frequency of excitation for which standing waves are observed with point A as a node is [L1=60cm,L2=86.6cm] density of aluminium =2.6g/cm3 and of steel=7.8g/cm3]
 A223HzB423HzC327 HzD427 Hz
A223HzB423HzC327 HzD427 HzA steel wire of diameter 1 mm, and length 2 m is stretched by applying a force of 2.2 kg wt. the extension produced in the wire is
A2.8×10−4mB2.8×10−6mC1.4×10−4mD1.4×10−6m
An aluminium wire of length 0.6 m and cross sectioal are and length 0.866 m .The compound wire is loaded with 10kg.Find the lowest frequency of exciation for which the joint In the the wire.The density of alumimium is 2600 kg m−3 and that of steel is 7800 kgm−3
View SolutionAn aluminium wire of length 0.6 m and cross-sectional area 10−6m2 is connected to a steel wire of the same crosssectional area and length 0.866 m. The compound wire is loaded with 10 kg. Find the lowest frequency of excitation for which the joint in the wire is a node. Also find the number ofnodes, excluding the two at the ends of the wire. The density of aluminium is 2600kg/m3 andthatofsteel is 7800kg/m3
View SolutionA metal wire of length jl and area of cross - section A is fixed between rigid supports negligible tension . If this is cooled. The tension in the wire will be
View SolutionA 40 cm wire having a mass of 3.2 g is stretched between two fixed supports 40.05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1.0mm2, find its Young modulus.
View SolutionA decrease in temperature of 40∘C produces a 0.1 % strain in a wire stretched between two fixed supports. If the area of cross section of the wire is πmm2 and Young's modulus of its material is 160 GPa, the thermal stress in the wire is
View Solution

