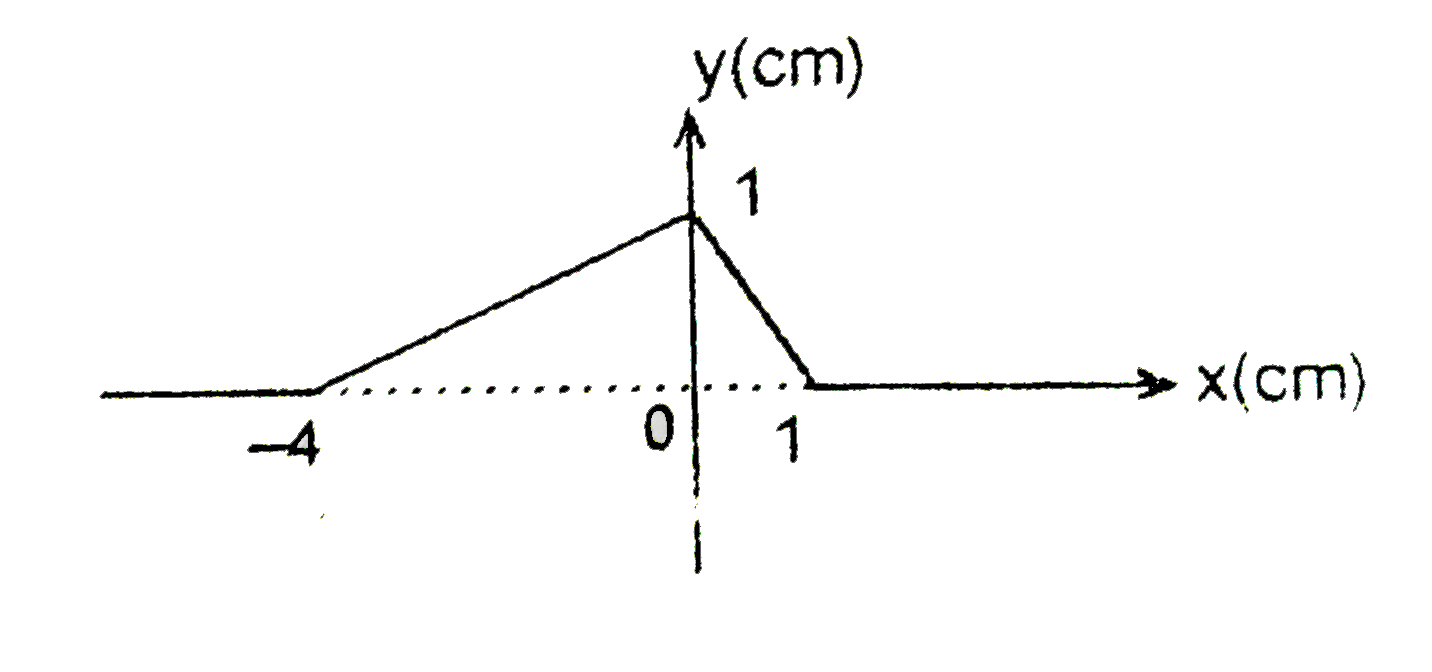
A pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪
⎪⎨⎪
⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
the shape of the string is drawn at t=0 and lthe area of the pulse elclosed by the string and the x−string is measured. It will be equal to
2cm2
2.5cm2
4cm2
5cm2
The correct Answer is:B
Shape of the pulse at t=0
That is a triangular pulse Area of the pulse
=12[(4×1)+(1×1)]
=52cm2
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 3 PART I
Explore 19 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 3 PART II
Explore 7 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 2 PART III
Explore 15 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
A hypothetical pulse is travelling along positive x direction on a taut string. The speed of the pulse is 10cms–1. The shape of the pulse at t = 0 is given as
y=x6+1for−6<x≤0=−x+1for0≤x<1=0for all other values of x
x and y are in cm.
(a) Find the vertical displacement of the particle at x = 1 cm at t = 0.2 s
(b) Find the transverse velocity of the particle at x = 1 cm at t = 0.2 s.
View SolutionA wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.
View Solution
Knowledge Check
A pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The vertical displacement of the particle of the string at x=7cm and t=0.01s will beA0.75cmB0.5cmC0.25cmDzeroA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The vertical displacement of the particle of the string at x=7cm and t=0.01s will beA0.75cmB0.5cmC0.25cmDzeroA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The transverse velocity of the particle at x=13cm and t=0.015s will beA−250cm/sB−500cm/sC500cm/sD−1000cm/s
A wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(ii) Shape of the pulse at t = 0 and t = 1s.
View SolutionA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The transverse velocity of the particle at x=13cm and t=0.015s will be
View SolutionA pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
There shape of the string is drawn at t=0 and the area of the pulse enclosed by the string the x-axis is measured. it will be equjal to
View SolutionA pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with {x−vt4+1forvt−4<x≤vt−(x−vt)+1forvt<x<vt+1
0, otherwise
{x−vt4+1forvt−4<x≤vt−(x−vt)+1forvt<x<vt+1
0, otherwise
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
The verticle displacement of the particle of the string at x=7cm and t=0.01s will be
View SolutionA pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
The transverse velocity of the particle at x=13cm and t=0.015s will be
View Solution

