A man generates a symmetrical pulse in a string by moving his hand up and down. At t=0 the point in his hand moves downward. The pulse travels with speed of 3m/s on the string & his hands passes 6 times in each second from the mean position. Then the point on the string at a distance 3m will reach its upper extreme first time at time t=
The correct Answer is:15
2f=6,f=3, T=13 sec, v=3m/sec
3=λT⇒λ=1m
x=vt
3=3t⇒t=1
total time =t+3T4=1+34(13)=54=1.25 sec.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART III
15 Videos
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART IV
9 Videos
- TRAVELLING WAVESBOOK - RESONANCECHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART I
21 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
- WAVE ON STRING BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART I
19 Videos
Similar Questions
A man gerates a symmetrical pulse in a strin by moving his hand up and down. At t=0 the point in his hand moves downward. The pulse travels with speed 3m/s on the string & his handsd pass 6 times in each second from the mean position. Then the point on the string t a distance 3m will reach its upper extreme first at time t=n/12. Find n
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=s, 2s and 3s.

View Solution
Knowledge Check
A string of length 0.4 m and mass 10−2 kg is clamped at its ends. The tension in the string is 1.6 N. When a pulse travels along the string the shape of the string is found to be the same at times t and t+△t. The value △t is
A0.05sB0.1sC0.2sD0.4sA wave pulse on a string has the dimension at time t=0 as shown below is reflected from a fixed end O.
Its dimensions at t=3s isA B
B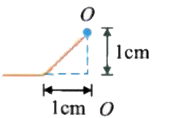 C
C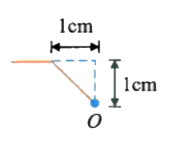 D
D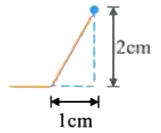
A pulse travelling at a speed of 2ms along the positive Z-axis is given by y =3z2+1 at t= 0 .The wave function representing the pulse at any times is given by
Ay=3(z−2t)2+1By=3(z+2t)2+1Cy=3(2z+t)2+1Dy=3(2z−t)2+1
A man travels half time of its journey with speed of 5m/s and for remaining half time he moves half of its total distance travelled, with speed of 3 m/s and remaining half distance with speed of 6 m/s. Find out the average speed of the man?
View SolutionA uniform string of length 6.5m is subjected to a tension of 40N. Mass of the string is 162.5g. One end of the string is fixed and the other end is tied to a source (s). which produces a transverse oscillation. The displacement of the end of the string tied to the source can be expressed as y=(3mm)sin(40πt), where ‘t’ is time. Find the displacement of point P of the string at a distance of 3.75m from the fixed end, at time t=0.3s.

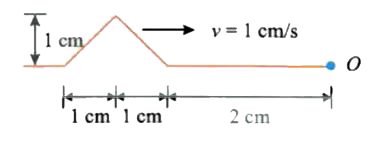
View SolutionA Wave pulse on a string has the dimension shown in figure. The waves speed is v=1 cm/s. If point O is a free end. The shape of wave at time t=3 s is:
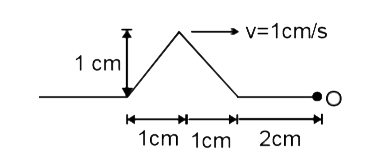
View SolutionThe equation of a wave pulse moving with a speed 1 m/sec at time t = 0 is given as y=f(x)=11+x2. Its equation at time t = 1 second can be given as
View SolutionFrom the origin at the same time two points being to move. The first moves on the X-axis at a speed =4 m/s, and the second on the Y axis at a spe3ed of 3 m/ sec.
View Solution
