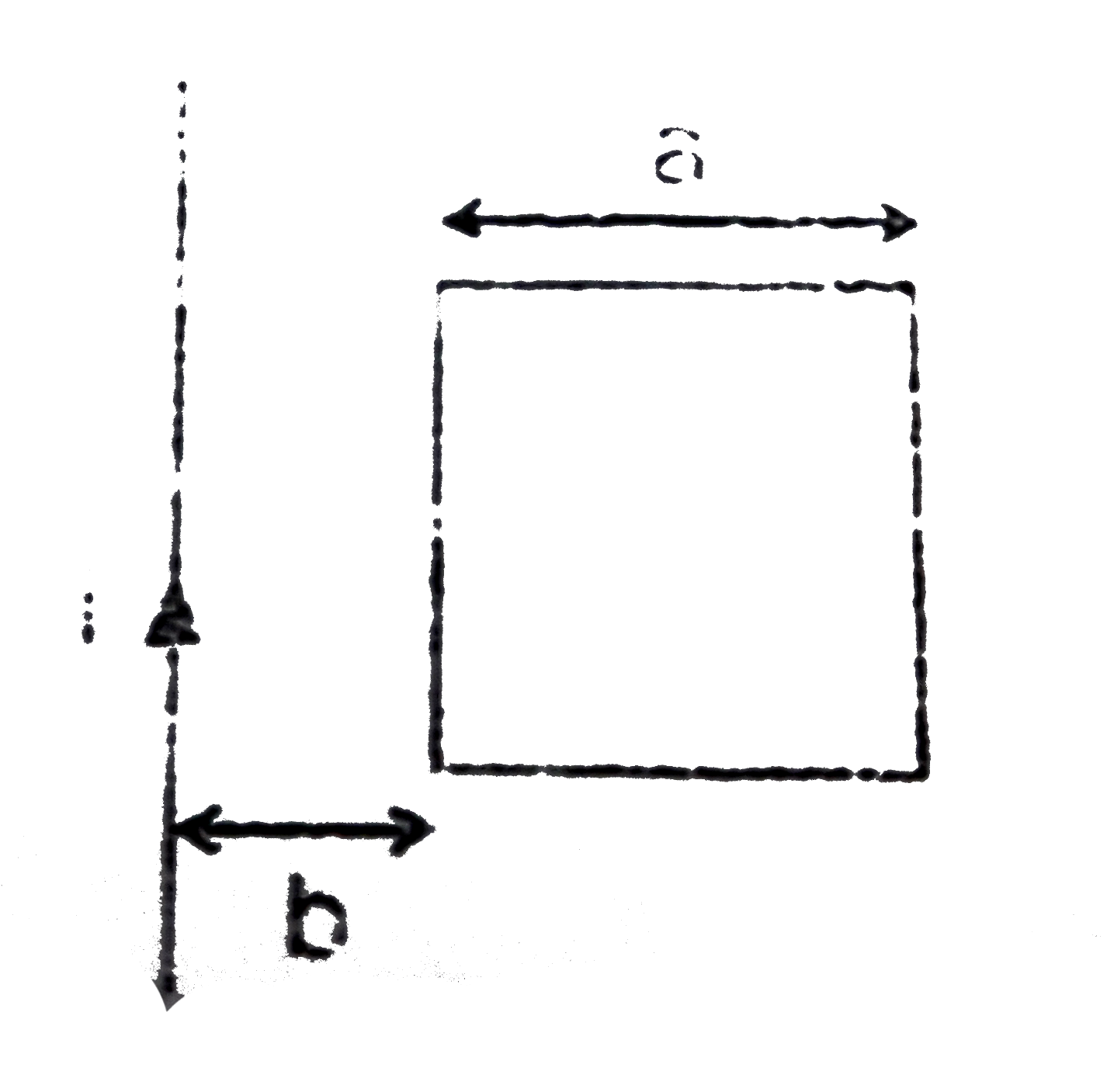
Figure showns a fixed square frame of wire having a total resistance r placed coplanarly with a long staight wire.The wire carries a current i given by i=i0cos(2πl/T).Find (a) the flux of the magnetic field through the square frame (b)the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to 10T.
The correct Answer is:A, B, C
(a)ϕ=∫B.ds
=a+b∫bμ0i2πr×adr=μ0ia2πln(a+bb)
(b)ε=−dϕdt=μ0ai02π2πTsin(2πt)Tln(a+bb)
(c)Q=10T∫0ε2rdt=(5μ20i20a2Tr)[ln(a+bb)]2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
Figure shows a fixed square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i=i0cos(2πt/T). Find (a) the flux of the magnetic field through the square frame , (b) the emf induced in the frame and ( c) the heat developed in the frame in the time interal 0 to 10T.
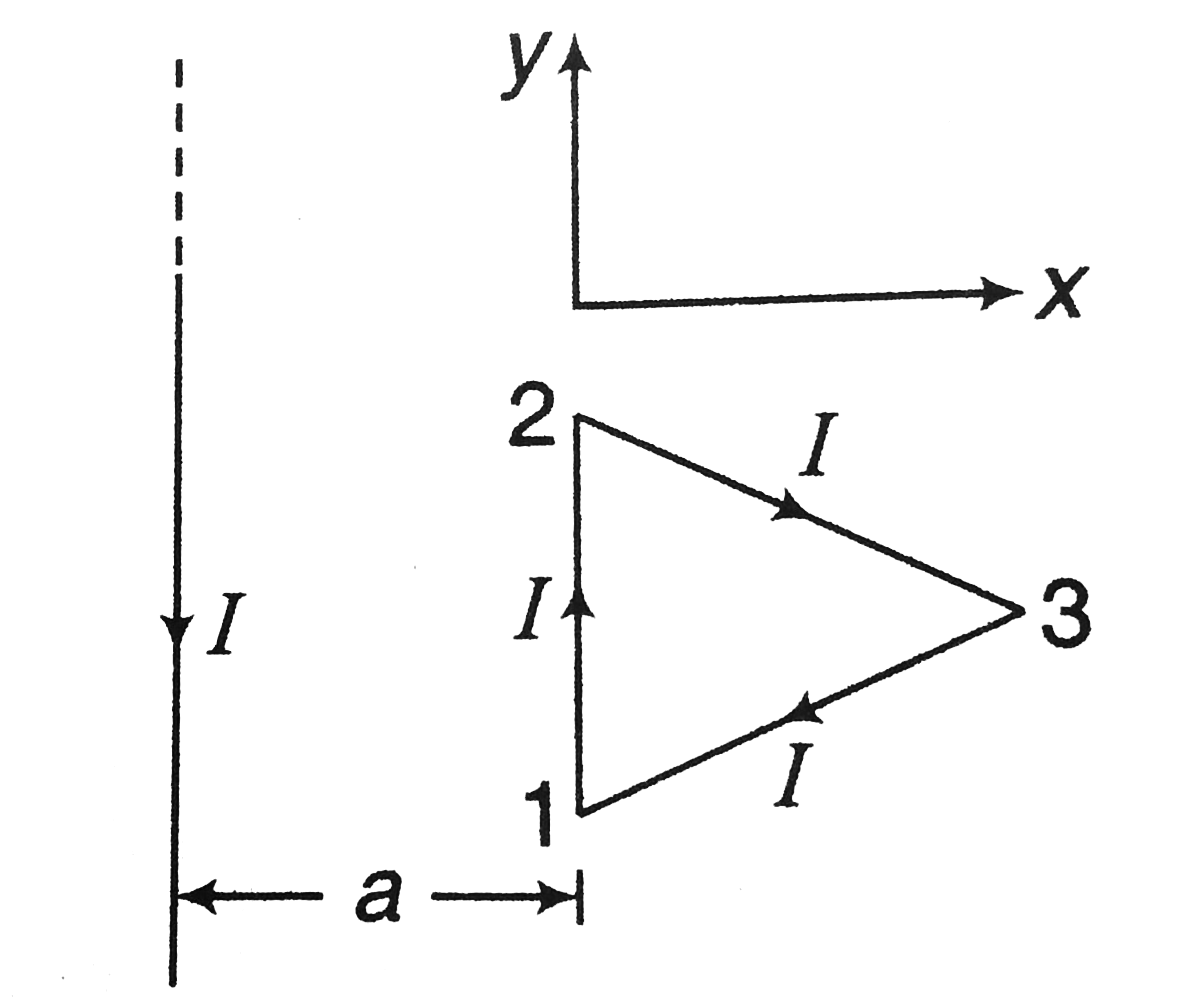
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
View Solution
Knowledge Check
A square frame of side 10 cm and a long straight wire carrying current 1 A are in the plane of the paper. Starting from close to the wire, the frame moves towards the right with a constant speed of 10ms−1 (sec figure). The e.m.f induced at the time the left arm of the frame is at x = 10 cm from the wire is
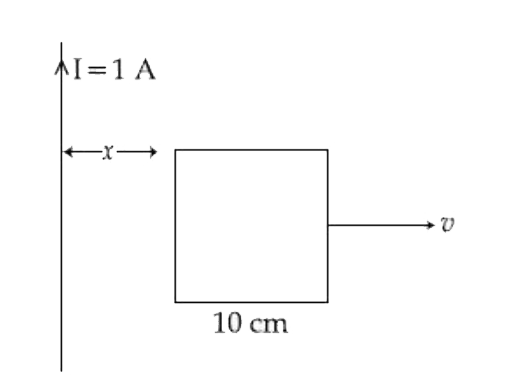 A0.75μvB1μvC2μvD0.5μv
A0.75μvB1μvC2μvD0.5μvA conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
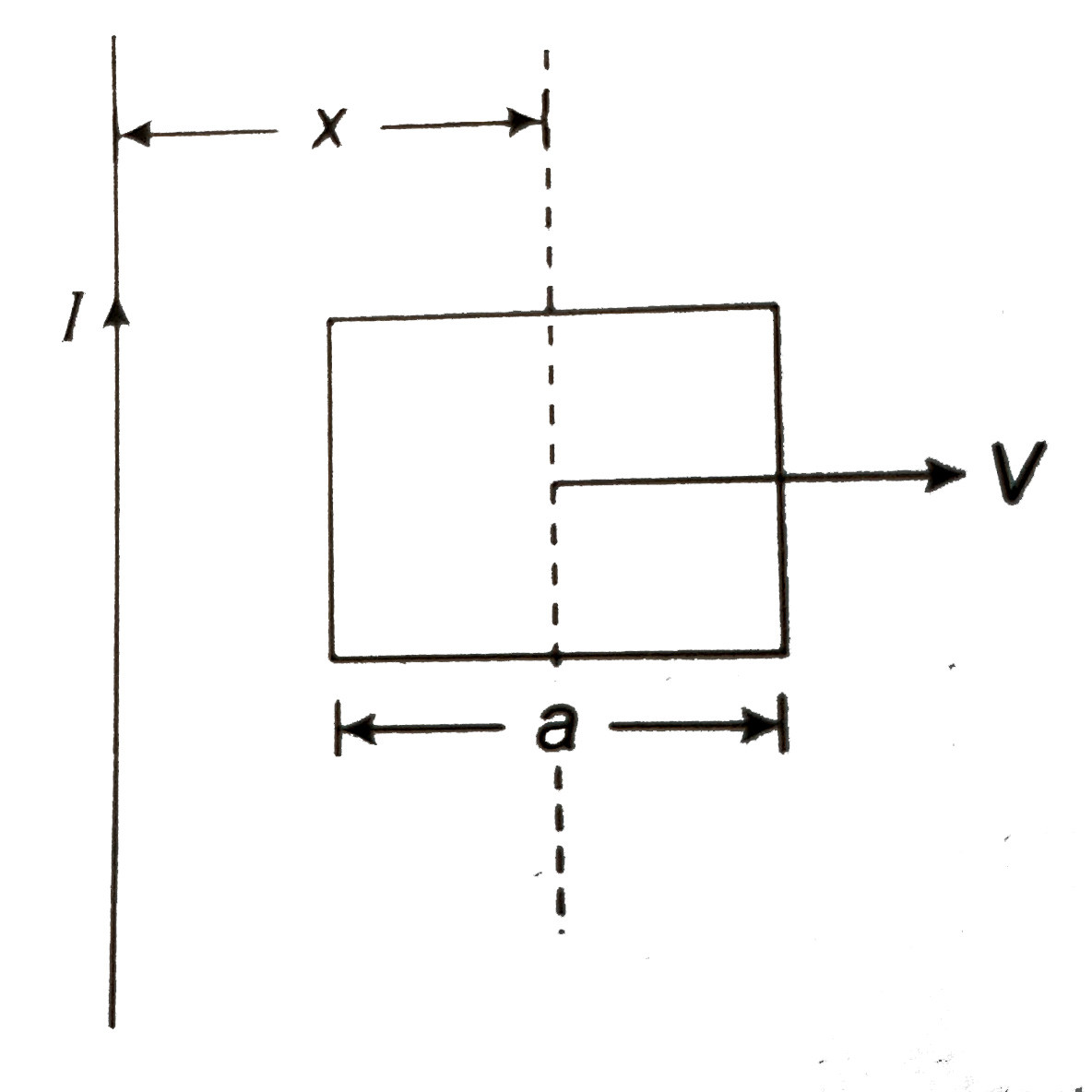 A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
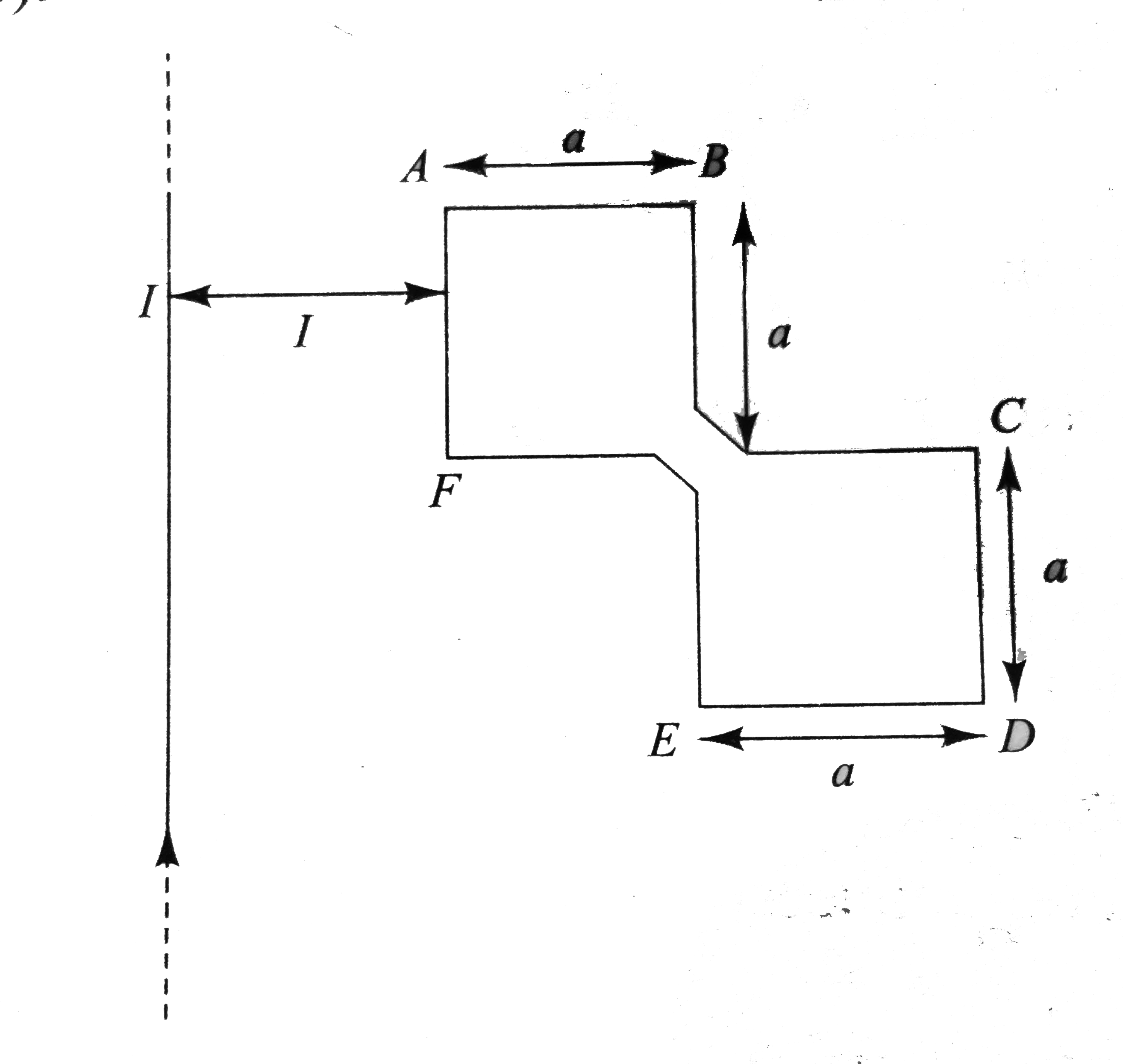
The heat produced in the loop in time t isA[μ0I02πIn(a+ll)]2at4λB[μ0I02πIn(2a+ll)]2at8λC[μ0I02πIn(a+ll)]2at3λD[μ0I02πIn(3a+ll)]2at6λ
A square frame of edge 10 cm is placed with its ositivae normal making on angle of 600 with a uniform electric field of 20Vm−1. Find the flux of the electric field through the surface bounded by the frame.
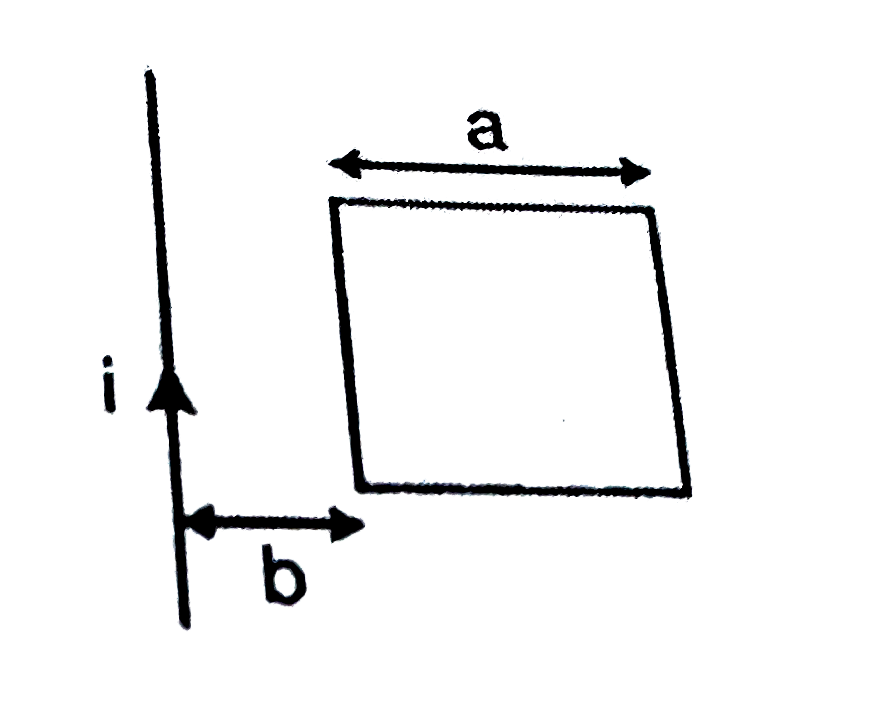
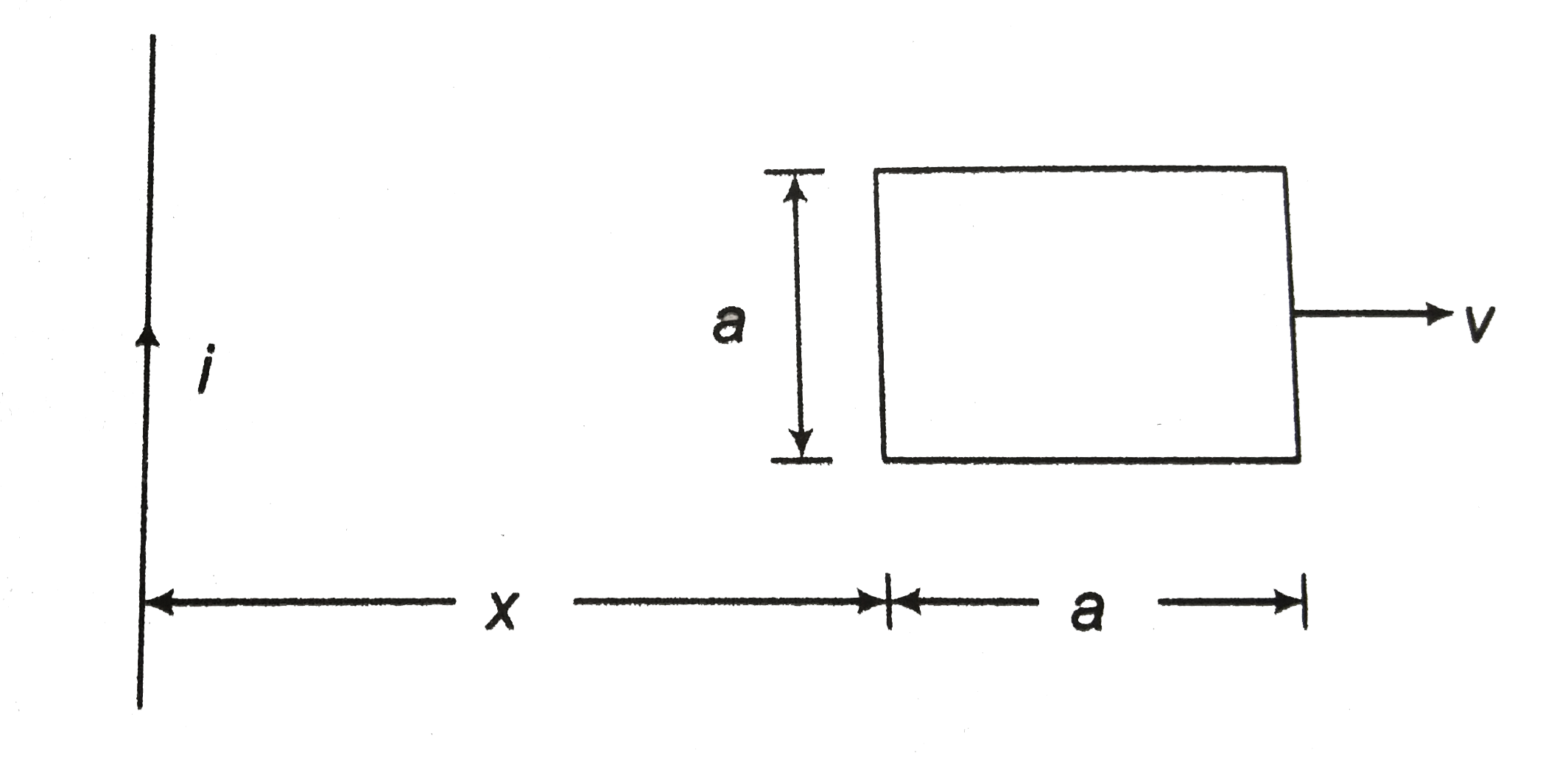
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionIn fig, a square loop consistaing of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varing current of magnitude I=(I0)cosωt but the direction of current in them are opposite
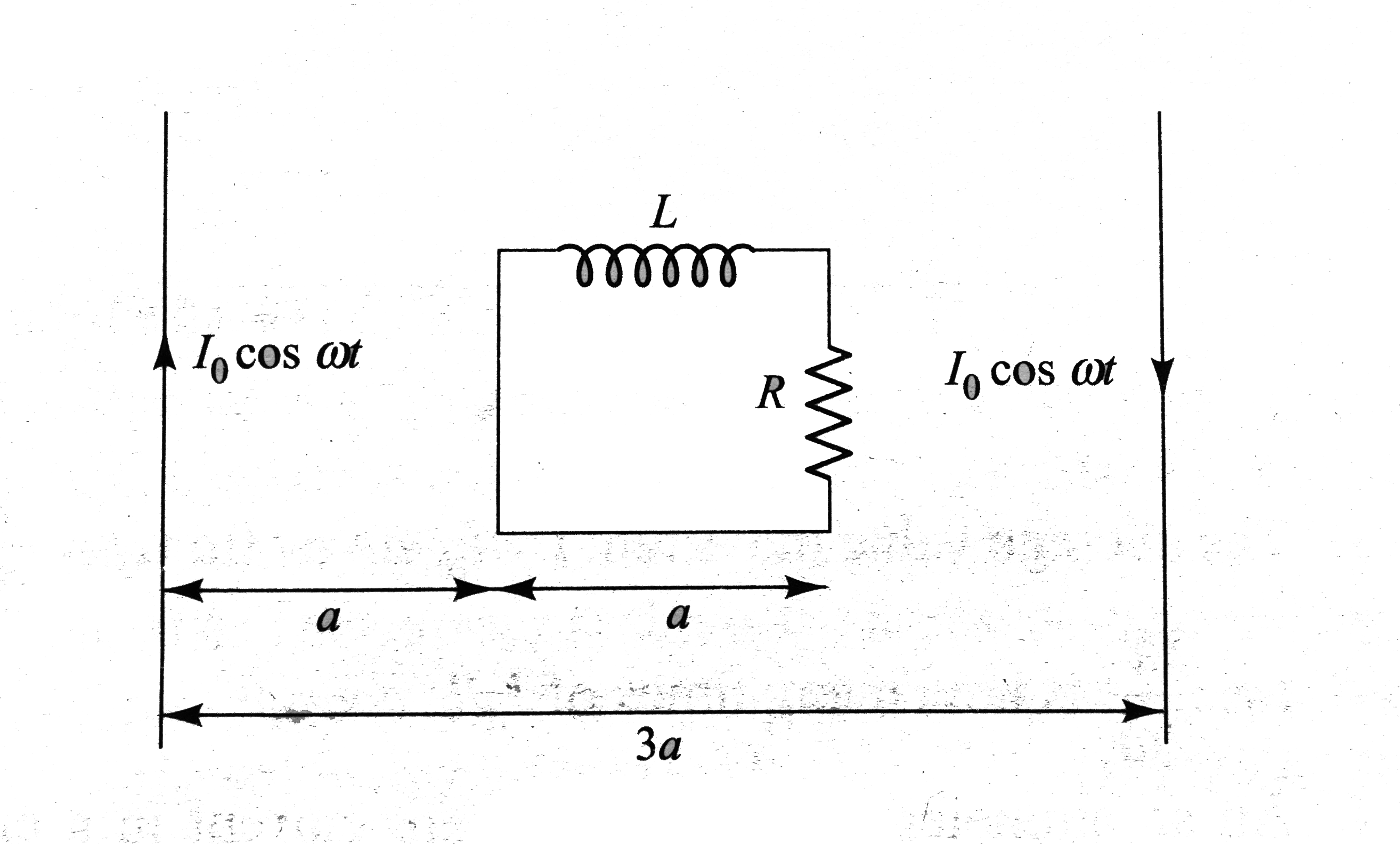
View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
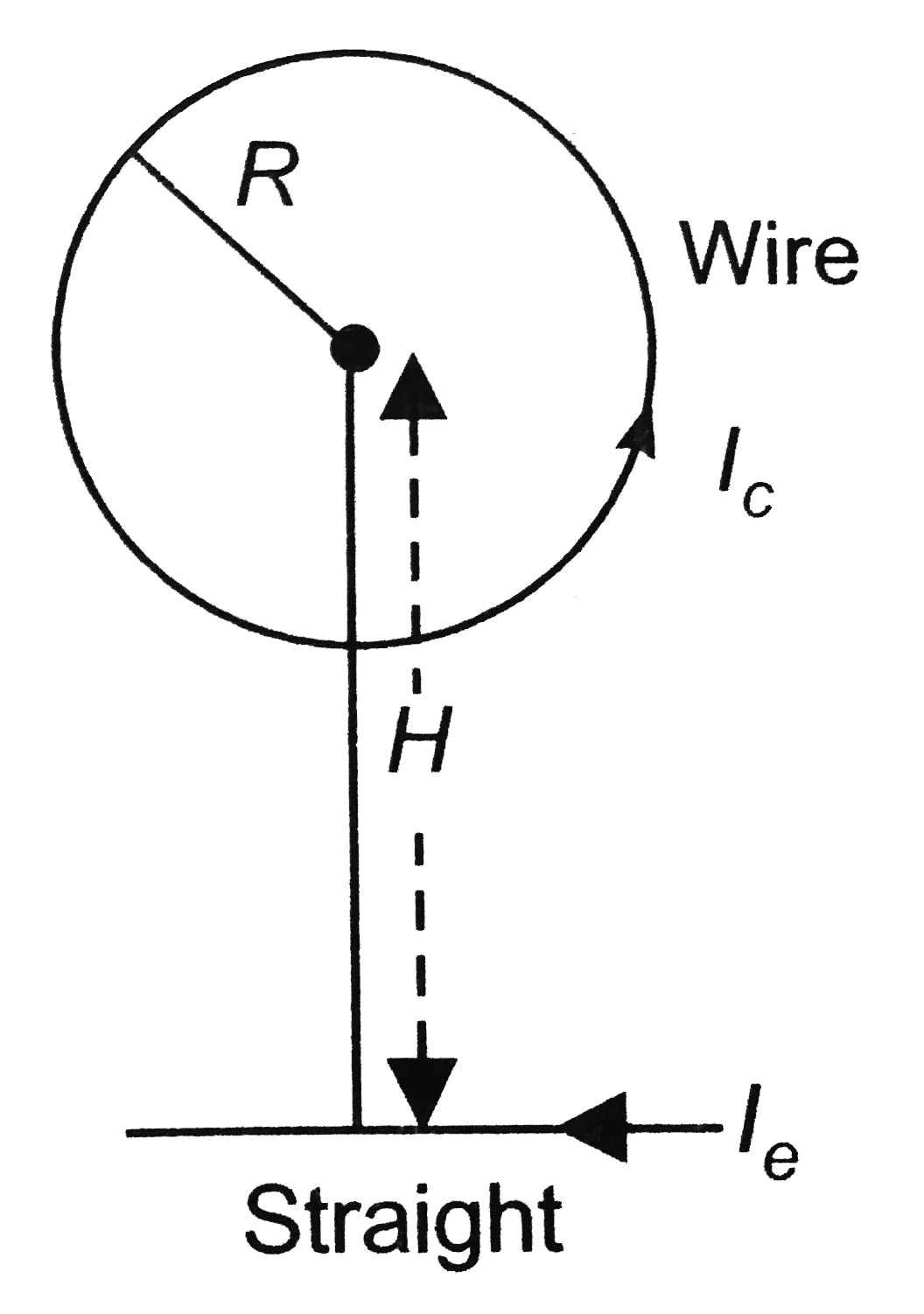
View Solution
