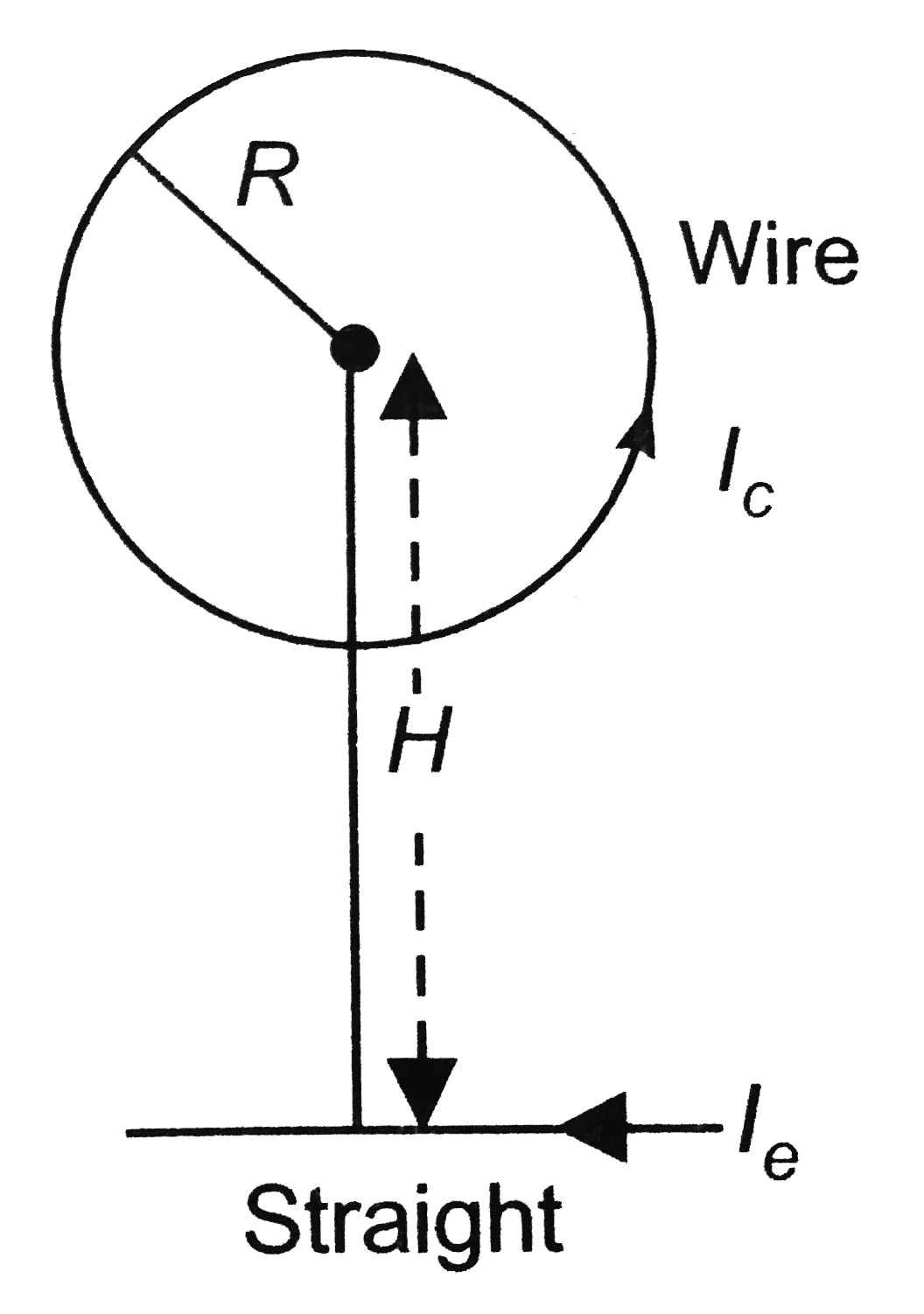
Circular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
IeRIcπ
IcRIeπ
πIcIeπ
IeπIcR
The correct Answer is:a
Magnetic field at the centre O of the loop of radius R is given by
B1=μ0Ic2R
where Ic is the current flowing in the loop. Magnetic field due to straight current carrying wire distance H, i.e., at the point O is given by
B2=μ0Ie2πH
For magnetic field to be zero at the centre of the loop,
B1=B2
i.e., μ0Ic2R=μ0Ie2πH
H=IeRπIc
Topper's Solved these Questions
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 2
45 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 3
44 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- NUCLEAR PHYSICSBOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
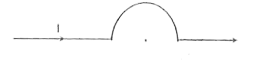
An infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
View SolutionA circular loop of radius r carries a current i. How should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View Solution
Knowledge Check
Circular loop of a wire and a long straight wire carry currents and respectively as shown in figure. Assuming that these are placed in the same plane, the magnetic fields will be zero at the centre of the loop when separation H Circular wire Straight wire
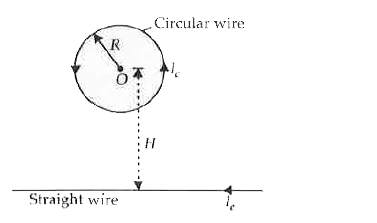 AIeRIcπBIcRIeπCπIcIcRDπIcIeR
AIeRIcπBIcRIeπCπIcIcRDπIcIeRA square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
Aμ0i4π8√a2+b2abBμ0i4π4√a2+b2abCμ0i4π2√a2+b2abDμ0i4π√a2+b2ab
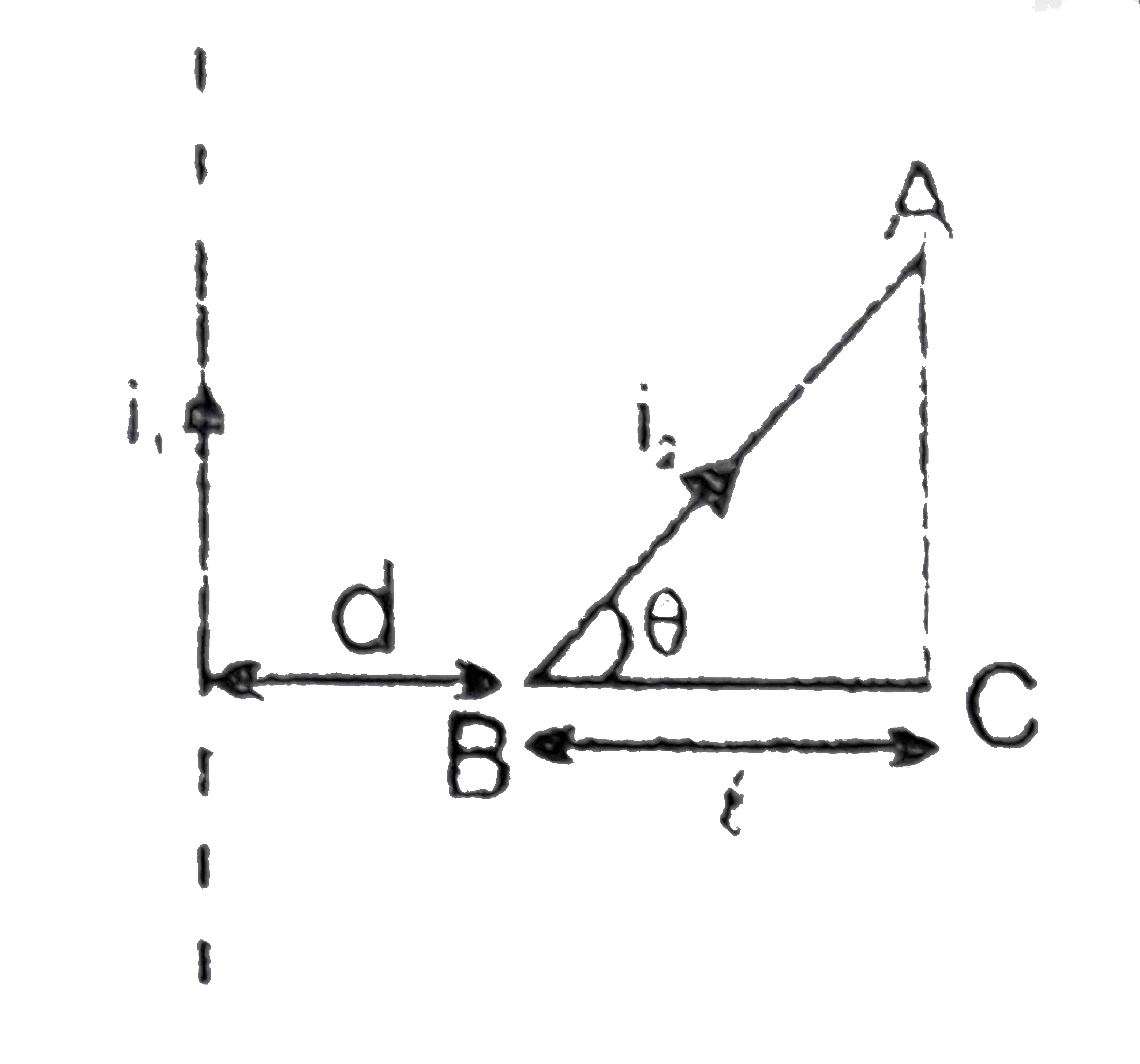
A triangular loop (ABC) having current i2 and an infinite wire having current i1 are placed in the same plane.Find the magnetic force of interaction between the infinite wire and the loop ABC.
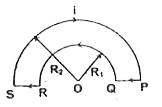
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
View SolutionA circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
View SolutionAn equilateral triangular loop of wire of side / carries a current I. The magnetic field produced at the circumcentre of the loop is
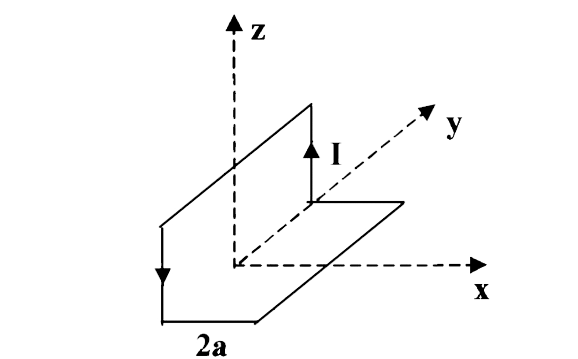
View SolutionA non - planar loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction
View Solution
