A coil $A B D$ of $N$ turns $&$ radius $R$ carries a current of $1 A m p$ $&$ is placed on a horizontal tabel. $K$ is a very small horizontal conducting ring of radius $r$ placed at a distance $Y_{0}$ from the centre of the coil vertically above the coil $A C D$ .Find an expression for the $E M F$ established when the ring $K$ is allowed to fall freely.Express the $E M F$ in terms of instanteous speed $v &$ height $Y$ .

Video Solution

Text Solution

Verified by Experts

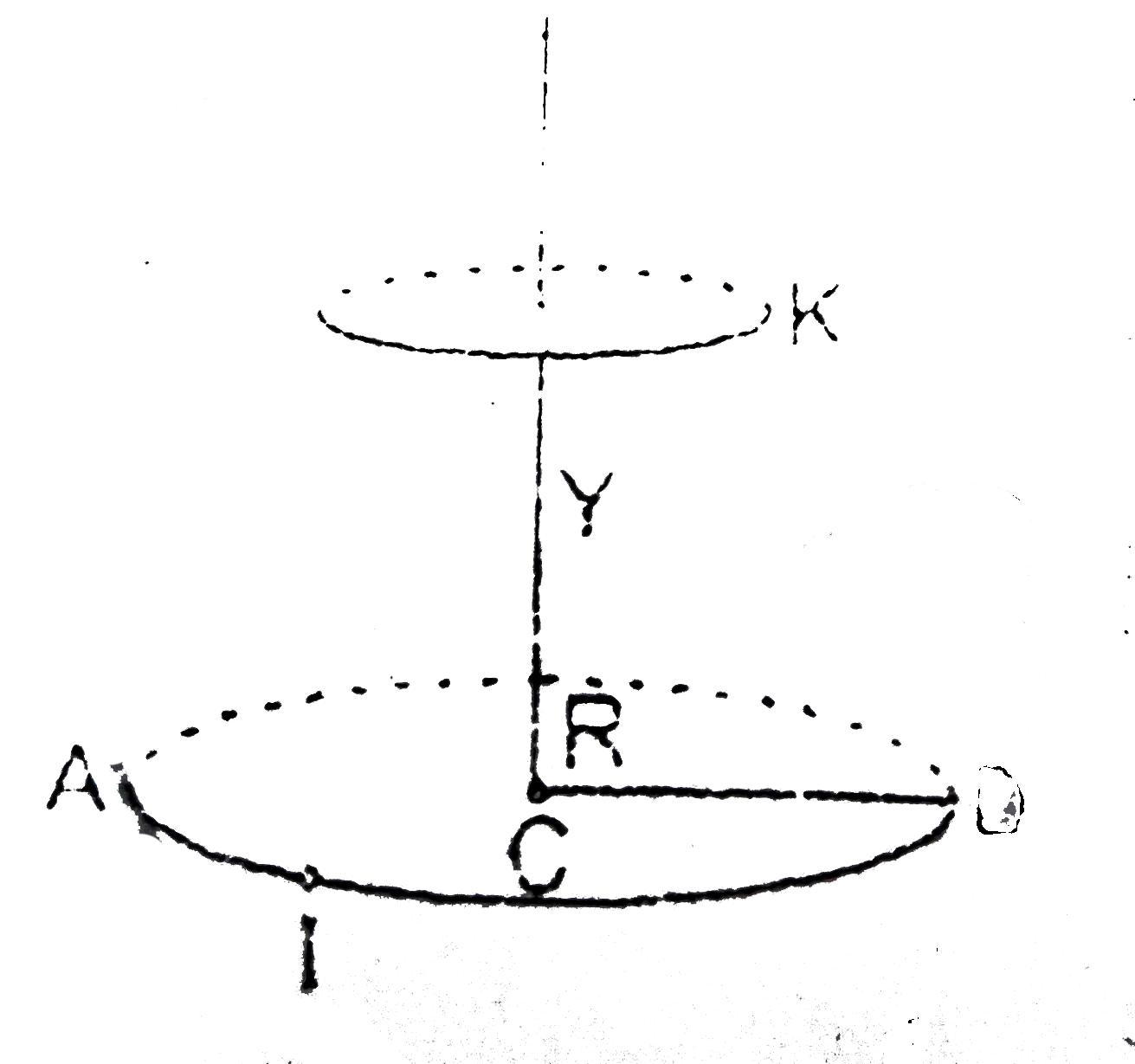
The correct Answer is:B, C

$B = \frac{μ_{0} I R^{2} N}{2 {[R^{2} + y^{2}]}^{3 / 2}}$
$ε = - \frac{d ϕ}{d t} = - A \frac{d B}{d t} = - π r^{2} \frac{d B}{d t}$ ...(1)
here $\frac{d B}{d t} = - \frac{μ_{0} I R^{2} N}{2} \times \frac{3}{2} \frac{1}{{[R^{2} + y^{2}]}^{5 / 2}} \times 2 y \times \frac{d y}{d t}$
$= - \frac{3 μ_{0} I R^{2} N}{2} \frac{y v}{{[R^{2} + y^{2}]}^{5 / 2}}$ put this value in eq. (i) and get Ans.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circular coil of n turns and radius r carries a current I. The magnetic field at the center is
A $\frac{μ_{0} n I}{r}$
B $\frac{μ_{0} n I}{2 r}$
C $\frac{2 μ_{0} n I}{r}$
D $\frac{μ_{0} n I}{4 r}$
Question 2 - Select One
The ratio of the magnetic field at the centre of a current carrying coil of the radius $a$ and at distance $' a'$ from centre of the coil and perpendicular to the axis of coil is
A $\frac{1}{\sqrt{2}}$
B $\sqrt{2}$
C $\frac{1}{2 \sqrt{2}}$
D $2 \sqrt{2}$
Question 3 - Select One
A circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that $r > > R$ , varies as
A $\frac{1}{r}$
B $\frac{1}{r^{3 / 2}}$
C $\frac{1}{r^{2}}$
D $\frac{1}{r^{3}}$

RESONANCE-ELECTROMAGNETIC INDUCTION-Exercis-1

Home
Ask Doubt
Profile