A liquid is filled in a spherical container of radius R up to a height h. At this position the liquid surface at the end is also horizontal. The contact angle is

0
cos−1(R−hR)
cos−1(h−RR)
sin−1(R−hR)
The correct Answer is:B
cosθ=R−hR
θ=cos−1(R−hR)

Topper's Solved these Questions
Similar Questions
(i) Water drops on two surfaces A and B has been shown in figure. Which surface is hydrophobic and which surface is hydrophilic?

(ii) A liquid is filled in a spherical container of radius R till a height h. In this position the liquid surface at the edges is also horizontal. What is the contact angle between the liquid and the container wall?

View SolutionA cylindrical vessel of radius R=1m and height H=3m is filled with an ideal liquid up to a height of h=2 m. the contaienr with liquid is rotated about its central vertical axis such that the liquid just rises to the brim. Calculate the angular speed (ω) of the container.
View Solution
Knowledge Check
A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−hIf x cubic units of a liquid is filled in n cylindrical shaped containers of radius rand height h then n =x/πr2h. If x cubic units of solid material is nr h consumed for making n spherical balls of radius r. Then n= 3x/4πr3
If 21560 cubic cm of a liquid is filled in some cylindrical shaped container of radius 7 cm and height 14 cm. Find the number of such containers.A5B10C15D7A liquid rises in a capillary tube of radius r upto height h and tha mass of liquid is 20 gm . If a the radius of capillary tube is half and height is twice , then the new mass of a liquid will be ,
A10 gmB80 gmC20 gmD40 gm
The radii of two columns in a U tube are r1andr2(r1>r2). A liquid of density ρ is filled in it. The contact angle of the liquid with the tube wall is θ. If the surface tension of the liquid is T then plot the graph of the level difference (h) of the liquid in the two arms versus contact angle θ. Plot the graph for angle θ changing from 0∘→90∘. Assume the curved surface of meniscus to be part of a sphere.

View SolutionA small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled in to the jar up to a certain height. The rate of dissension of liquid is independent of level of the liquid in the jar. Then the surface of jar is a surface of revolution of curve

View SolutionA liquid does not wet solid surface if angle of contact is
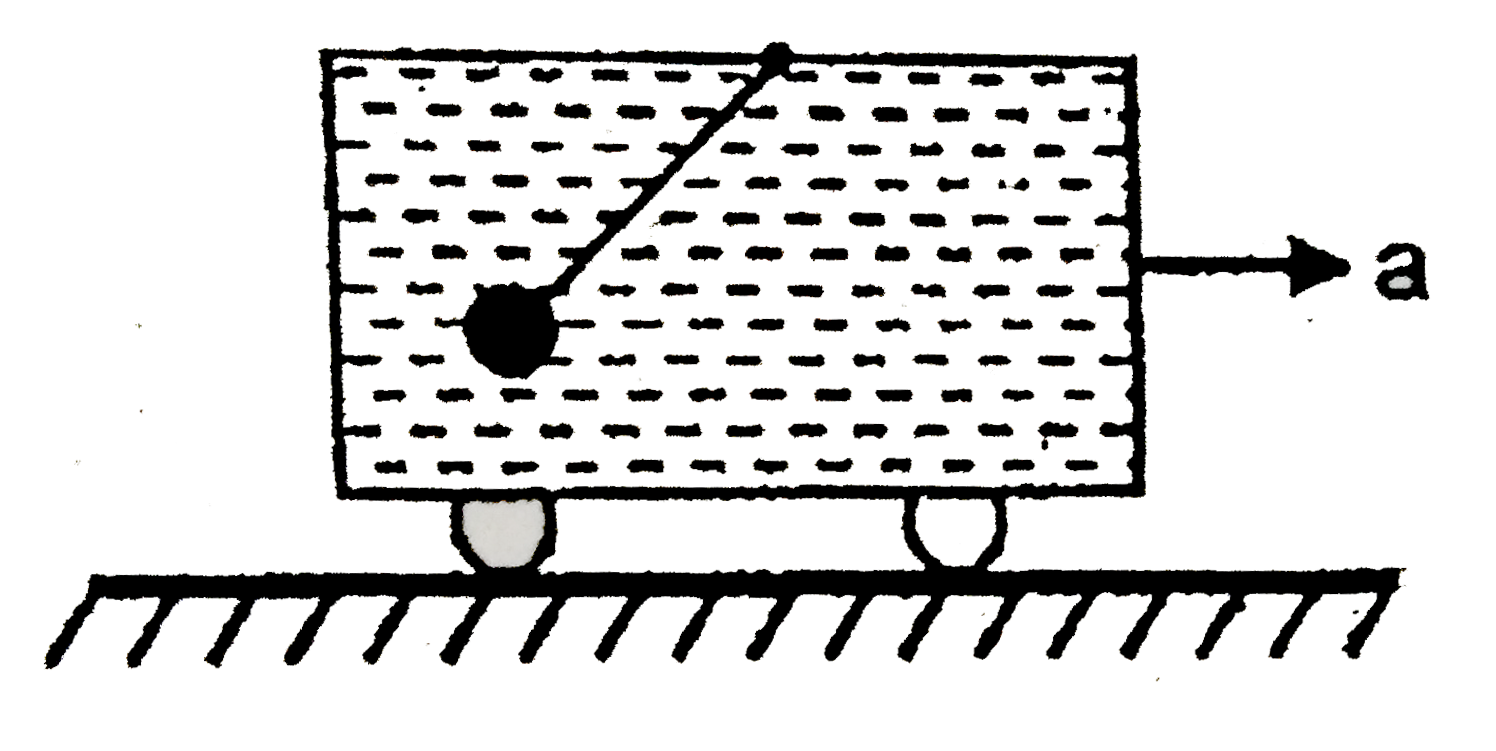
View SolutionFigure shows a closed container completely filled with an ideal liquid of density ρ. In the liquid there is a spherical body of volume V and density σ attached to a string whose other end is attached to the roof of the container. The container is accelerating with an acceleration 'a' towards right. The force exerted by the liquid on the spherical body when it is in equillibrium with respect to the liquid, will be :
View SolutionA spherical liquid drop of radius R is split up ino 8 equal droplets .If T is the surface tension of the liquid , then the work done in this process is
View Solution

