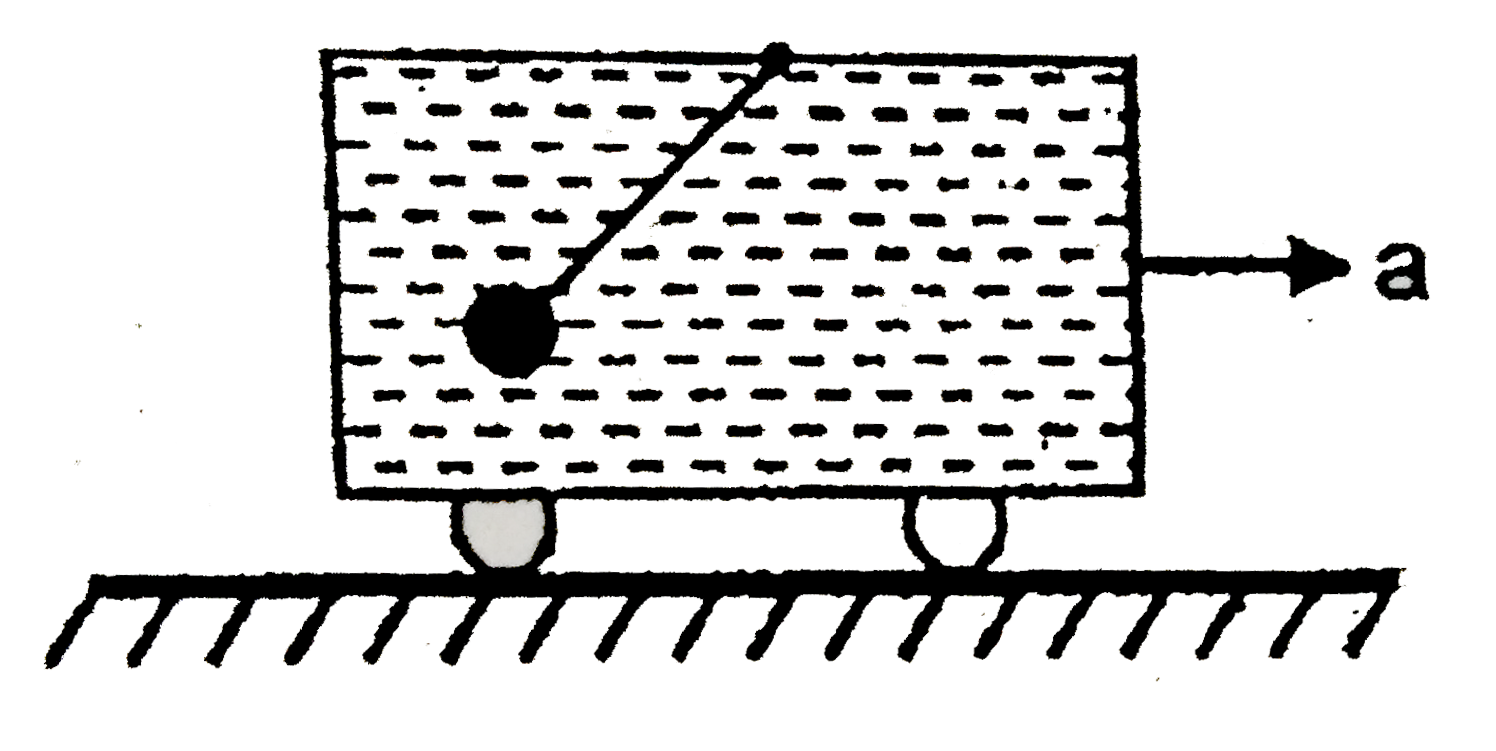
Figure shows a closed container completely filled with an ideal liquid of density ρ. In the liquid there is a spherical body of volume V and density σ attached to a string whose other end is attached to the roof of the container. The container is accelerating with an acceleration 'a' towards right. The force exerted by the liquid on the spherical body when it is in equillibrium with respect to the liquid, will be :
Vρ√a2+g2+Vσa
Vρg+Vσa
Vρ(g+a)
Vρ√a2+g2
The correct Answer is:D
From the frame of reference of liquid, effective gravity (resultant of weight and pseudo force per unit mass) =√a2+g2
∴ Effective force due to liquid =Vρ√a2+g2
Aliter: The force exerted on spherical body by surrounding liquid is equal to sum of contact forces on displaced liquid by the surrounding liquid as shown in
Hence force exerted on spherical body
by surrouding liquid =Vρ√a2+g2

Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Examples
22 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise
18 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
A body sinks in a liquid if its density is ________the density of the liquid.
View SolutionA wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
View Solution
Knowledge Check
The pressure exerted by a liquid column at the bottom of the liquid container is
Adoes not depend on the area of cross-section of container.Bdependent on the density of the liquid.Cequal in all directions.DAll the above are trueA body having volume V and density ρ is attached to the bottom of a container as shown. Density of the liquid is d(>ρ). Container has a constant upward acceleration a. Tension in the string is
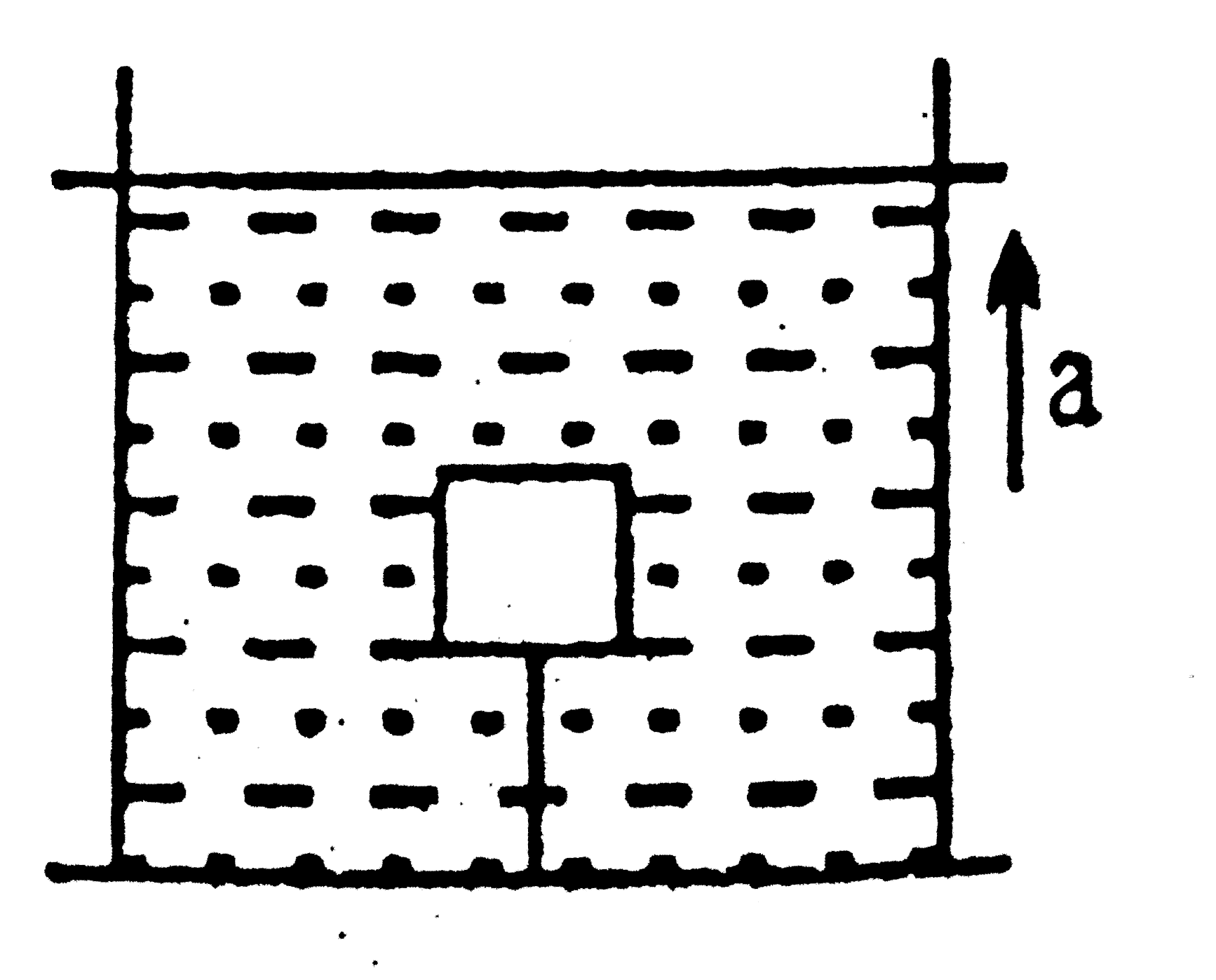 AV[Dg−ρ(g+a)]BV(g+a)(d−ρ)CV(d−ρ)gDnone
AV[Dg−ρ(g+a)]BV(g+a)(d−ρ)CV(d−ρ)gDnoneA body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
AVdgBVρgCV(ρ−d)gDV(d−ρ)g
A liquid is filled in a container is accelarated towards right. There are four points A,B,C and D in the liquid. Choose the correct options.

View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
View SolutionLiquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
View SolutionA container shown in figure contains a liquid to depth H, and of density ρ The gauge pressure at point P is :
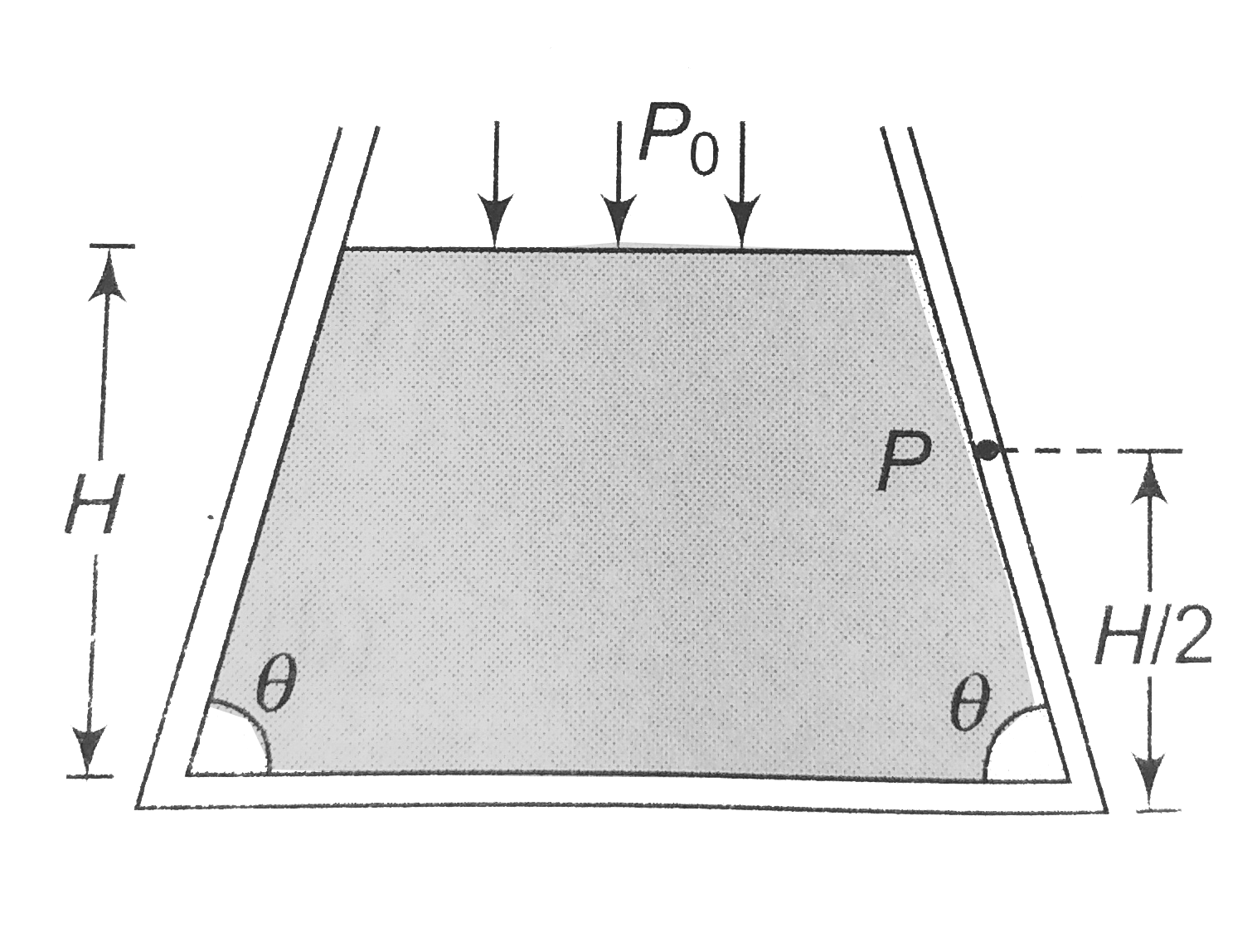
View Solution
