A container of cross-section area 'S' and height 'h' is filled with mercury up to the brim. Then the container is sealed airtight and a hole of small cross section area 'S/n' (where 'n' is a positive constant) is puched in its bottom. Find out the time interval upto which the mercury will come out from the bottom hole.
[Take the atmospheric pressure to be equal to h0 height of mercury column: h>h0]
The correct Answer is:14T∫0dt;t=n√2g(h−h0)
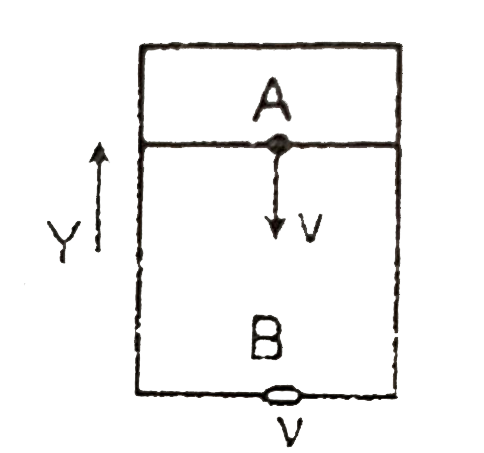
Let the velocity of effiux of mercury coming out of hole be v at an instant mercury level in container is y. aT same instant the speed of top surface of fluid v. From equilibrium of continuity
Snv=Sv….(1)
∵Sn<<S∴v>>v
applying Bernoulli's theorem between A and B
Yeg+12ev3=Patm+12ev2
∵v<<v higher powers of v can
be neglected and Patm=h0eg
∴v=√2g(Y−h0)......(2)
Hence mercury flows out of both till y=h0.
from equation (1)
v=−dydt=1hv=1h√2g(Y−h0)
or −dy√2gY−h0=1hdt
integrading between limits
at l=0y=n and t=T,Y=h0,−h0∫n−dy√2g(Y−h0)=1h=1nT∫0dt,t=n√2g(h−h0)
Topper's Solved these Questions
Similar Questions
Consider the barometer shown in figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?

View SolutionA cylindrical tank of cross sectional area a1 is filled with water to a height h. A hole of cross sectional area a2 is made at the bottom. If a1=5a2, then find the
(i) initial velocity with which the water falls in tank.
(ii) initial velocity with which water emerges out from hole.
(iii) time taken to make the tank empty.
View Solution
Knowledge Check
A 1.00 m tall container is filled to the brim , partway with mercury and the rest of the way with water . The container is open to the atmosphere . What must be the depth of the mercury so that the absolute pressure on the bottom of the container is twice the atmospheric pressure ?
A0.74 mB0.88 mC0.43 mD0.52 mA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2Consider the barometer shown in figure. Density of mercury is ρ. A small hole is made at point S as shown. The mercury come out from this hole with speed v equal to
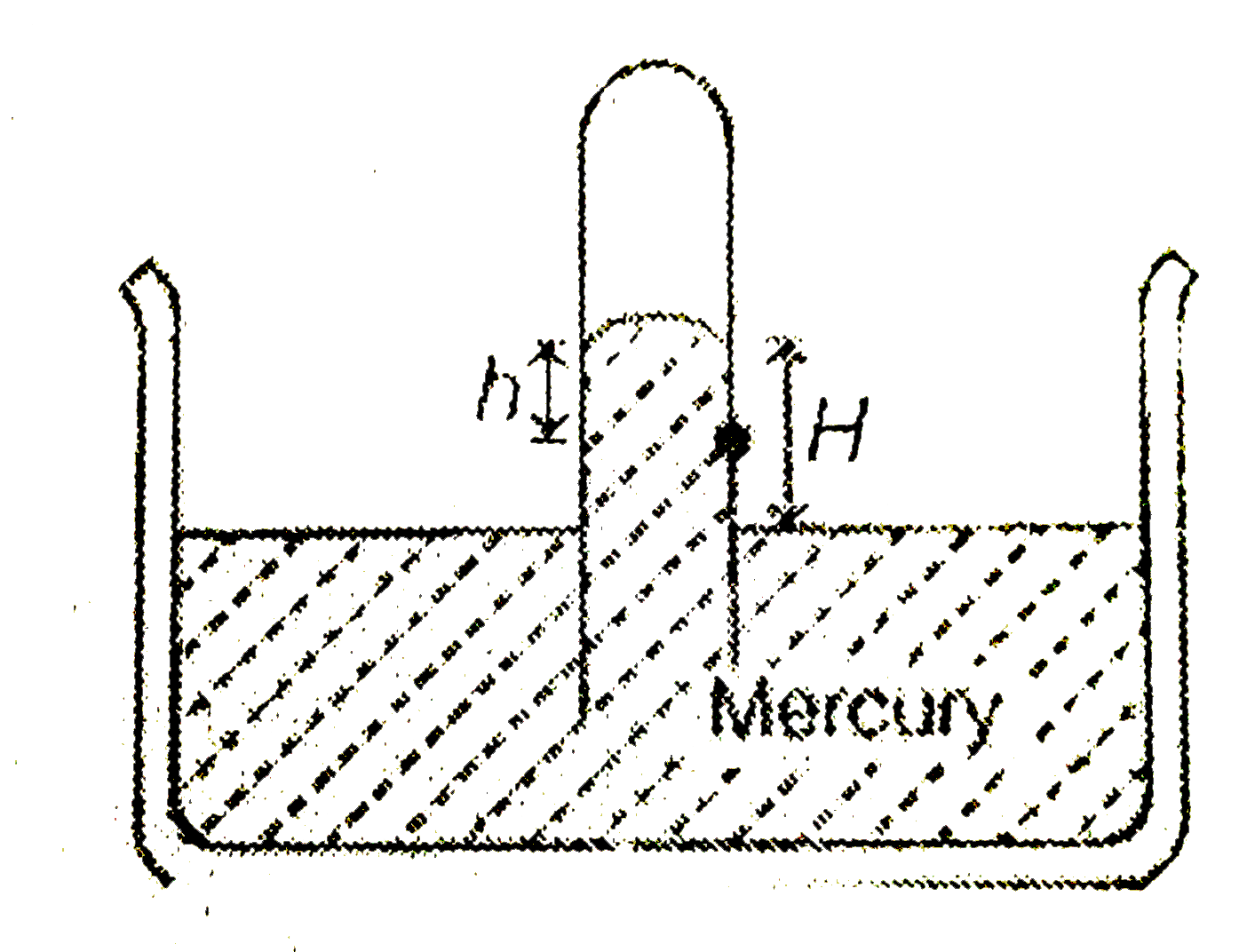 A√2ghB√2gHC√2g(H−h)DNone of these
A√2ghB√2gHC√2g(H−h)DNone of these
A cylindrical vessel of cross section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionOil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution
