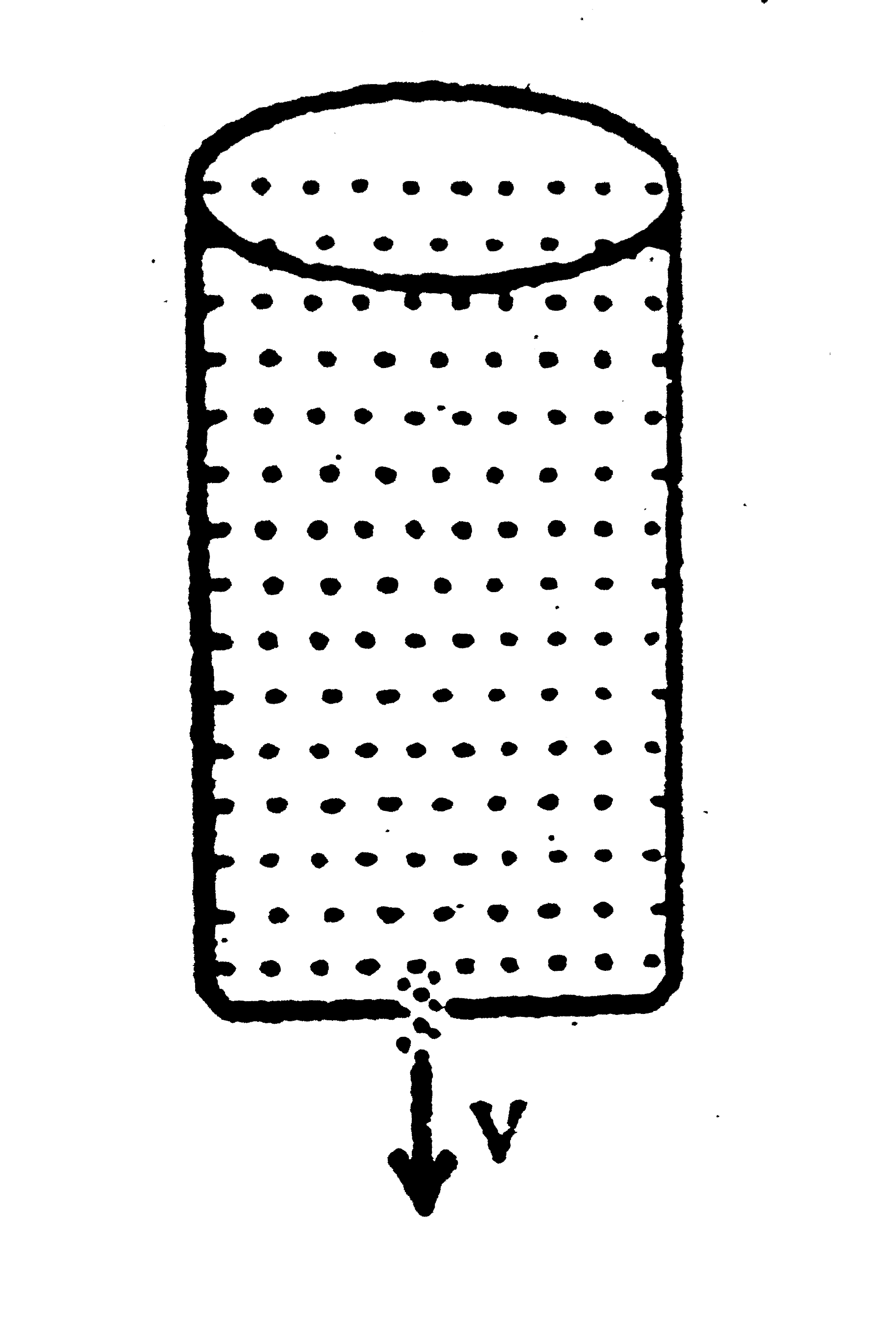
A cylindrical vessel open at the top is 20cm high and 10cm in diameter. A circular hole of cross-sectional area 1cm2 is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate of 102cm3/s. The height of water in the vessel under steady state is (Take g=10m/s2).
The correct Answer is:5cm
V=a.v==⇒V=a√2gh100=1√2×1000×hh=102h=5cm
Topper's Solved these Questions
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # II
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # III
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
Similar Questions
A cylindrical bucket, open at the top, is 0.200 m high and 0.100 m in diameter. A circular hole wih cross-section area 1.00cm2 is cut in the centre of the bottom of the bucket. Water flows into the bucket from a tube above it at the rate of 1.30×10−4m3/s. How high will the water in the bucket rise?
View SolutionA cylindrical vessel, open at the top, has a radius 10 cm and height 14 cm. Find the total surface area of the vessel. (Take pi = 3.14)
View Solution
Knowledge Check
A cylindrical tank has a hole of 2cm2 at its bottom if the water is allowed to flow into tank from a tube above it at the rate of 100cm3/s then find the maximum height upto which water can rise in the tank (take =g=10ms−2)
A2.5×10−2mB1.25×10−2mC5.5×10−2mD3.5×10−2mA cylindrical vessel of radius R and height H and open at the top is completely filled with y . A small circular hole of radius r is made near the bottom of vessel . The time taken for 25 % of water to flow out is
A√2Hg(√3−1)BR2r2√2Hg(1+2√3)CR2r2√2Hg(1−2√3)DR2r2√2Hg(√3−1)The level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
A10−2m3s−1B102m3s−1C10m3s−1D10−4m3s−1
A cylindrical vessel open at the top has diameter 20cm and height 14cm. Find the cost of tin-plating it on the inside at the rate of 50 paise per hundred square centimeter.
View SolutionA cylindrical vessel of height 10cm has base radius 60cm. If d is the diameter of a spherical vessel of equal volume, then what is d equal to
View SolutionA tank of height 5 m/s completely filled with water. There is a hole of cross sectional area 1cm2 near its bottom. What is the initial volume of water that will come out of the hole per second. (Use g=10m/s2)
View SolutionA tube 1cm2 in cross = section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g=msI(−2) Now.

View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
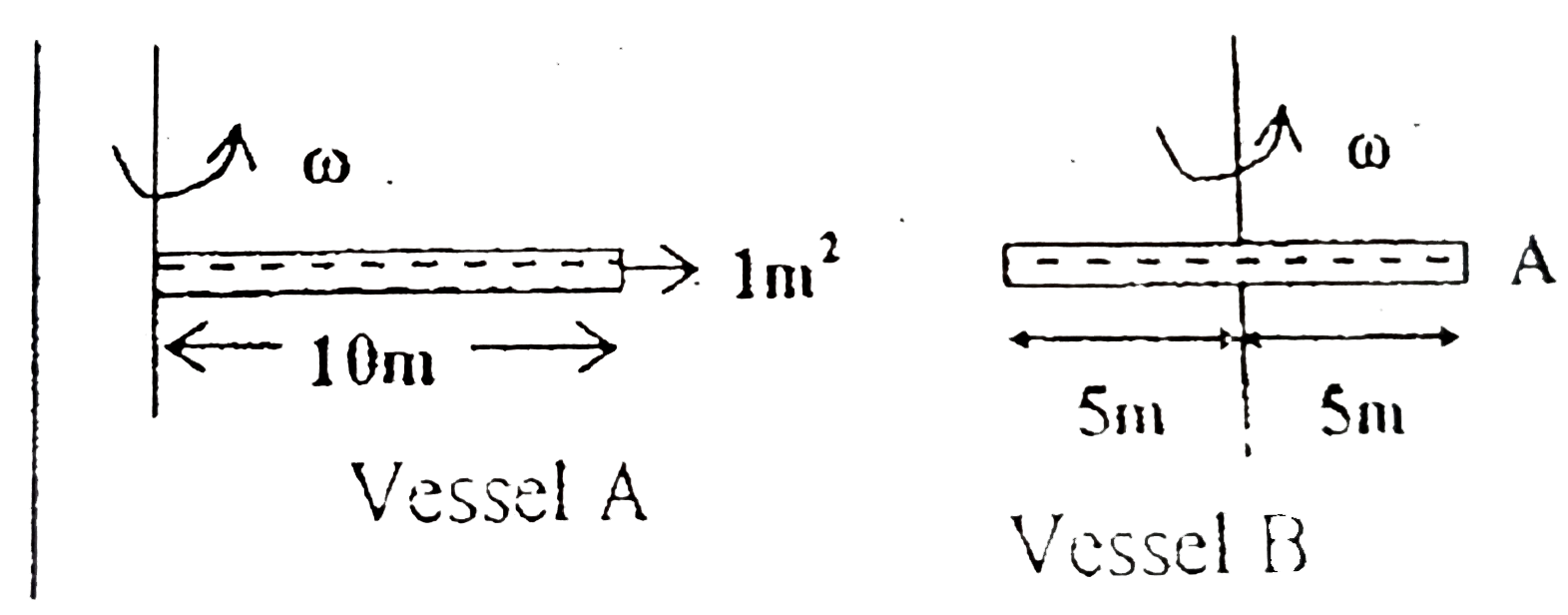
View Solution

