An expansible balloon filled with air floats on the surface of a lake with 2/3 of its volume submerged. How deep must it be sunk in the water so that it is just in equilibrium neither sinking further nor rising? Is is assumed that the temperature of the water is constant & that the height of the water barometer is 9 meters.
The correct Answer is:4.5 m
Let mass of air in ballon is m and its volume at surface is V.
mg=B =mg=23Vρwg ⇒V=32mcm3
at depth d below let its volume is V2
W=B ⇒mg=V2ρwg ⇒⇒V2=mcm3
Since P1V1=P2V2
9×32m=(9+d)×m ⇒d=4.5m
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - EXERCISE # II
18 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - EXERCISE # III
18 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
Similar Questions
An expansible balloon filled with air is floating on the top surface of a lake, with 2/3 of its volume is submerged in water. How deep should it be sunk in water without changing the temperature of air in it, in order that it is just in equilibrium, neither sinking nor rising further? Height of water barometer =10m.
View SolutionA sealed balloon, filled with air, floats in water with 13 of its volume submerged. It was found that if it is pushed inside water at a depth h, it remains in equilibrium, neither sinking nor rising. Find h. Given that height of water barometer is 10m and temperature is constant at all depth.
View Solution
Knowledge Check
A block of ice on earth floats on water with 9//10 of its volume submerged.
Statement-1: On moon the block of ice would float on water with less than 9//10 of its volume submerged.
Statement-2: The acceleration due to gravity on moon surface is less than that on earth.AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.When an air bubble of radius 'r' rises from the bottom to the surface of a lake, its radius becomes 5r/4 (the pressure of the atmosphere is equal to the 10m height of water column). If the temperature is constant and the surface tension is neglected, the depth of the lake is
A3.53mB6.53mC9.53mD12.53mAn air bubble rises from the bottom to the surface of lake and it is found that its diameter is duubled. If the height of water barometer is 11m, the depth of the lake in maters is
A70mB77mC7.7mD78m
A small piece of wood is floating on the surface of a 2.5 m deep lake. Where does the shadow form on the bottom when the sun is just setting? Refractive index of water = 4/3
View Solutionwhen an air bubble rises from the bottom to the surface of a lake, its radius becomes double . Find the depth of the lake , given that the atmospheric pressure is equal to the pressure due to a column of water 10 m high. Assume constant temperature and disreged surface tension .
View SolutionA narrow tube of length l and radius r is sealed at one end. Its open end is brought in contact with the surface of water while the tube is held vertical. The water rises to a height h in the tube. The contact angle of water with the tube wall is θ, density of water is ρ and the atmospheric pressure is Po. Find the surface tension of the liquid. Assume that the temperature of air inside the tube remains constant and the volume of the meniscus is negligible.
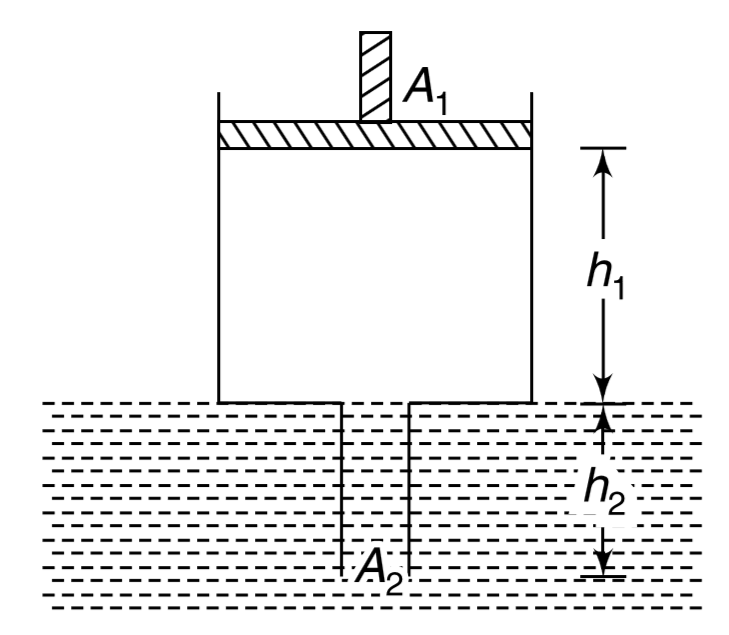
View SolutionA syringe has two cylindrical parts of cross sectional area A1=4cm2 and A2=1cm2. A mass less piston can slide on the inner wall of the part having cross section A1. The end of the part having cross section A2 is open. Syringe is dipped in a large water tank such that the narrower part remains completely submerged and the wider part is filled with air. The length shown in figure are h1=55cm and h2=100 cm. The piston is pushed down by a distance x such that 25% of the air inside the syringe is expelled out through the open end of the narrower part. Assume that the temperature of air remains constant and calculate x.
Density of water = 103kgm–3,g=10ms–2, Atmospheric pressure = 105Nm–2.
View SolutionAn air bubble starts rising from the bottom of a lake and its radius is doubled on reaching the surface. If the temperature is costant the depth of the lake is. (1 atmospheric pressure =10m height of water column)
View Solution
