A particle is projected with a velocity v so that its range on a horizontal plane is twice the greatest height attained. If g is acceleration due to gravity, then its range is
4v25g
4g5v2
4v35g2
4v5g24v5g2
The correct Answer is:A
R=2H⇒tanθ=42=2
R=2V3gsinθcosθ
R=2v2gXx2√5×1√5=4v25g
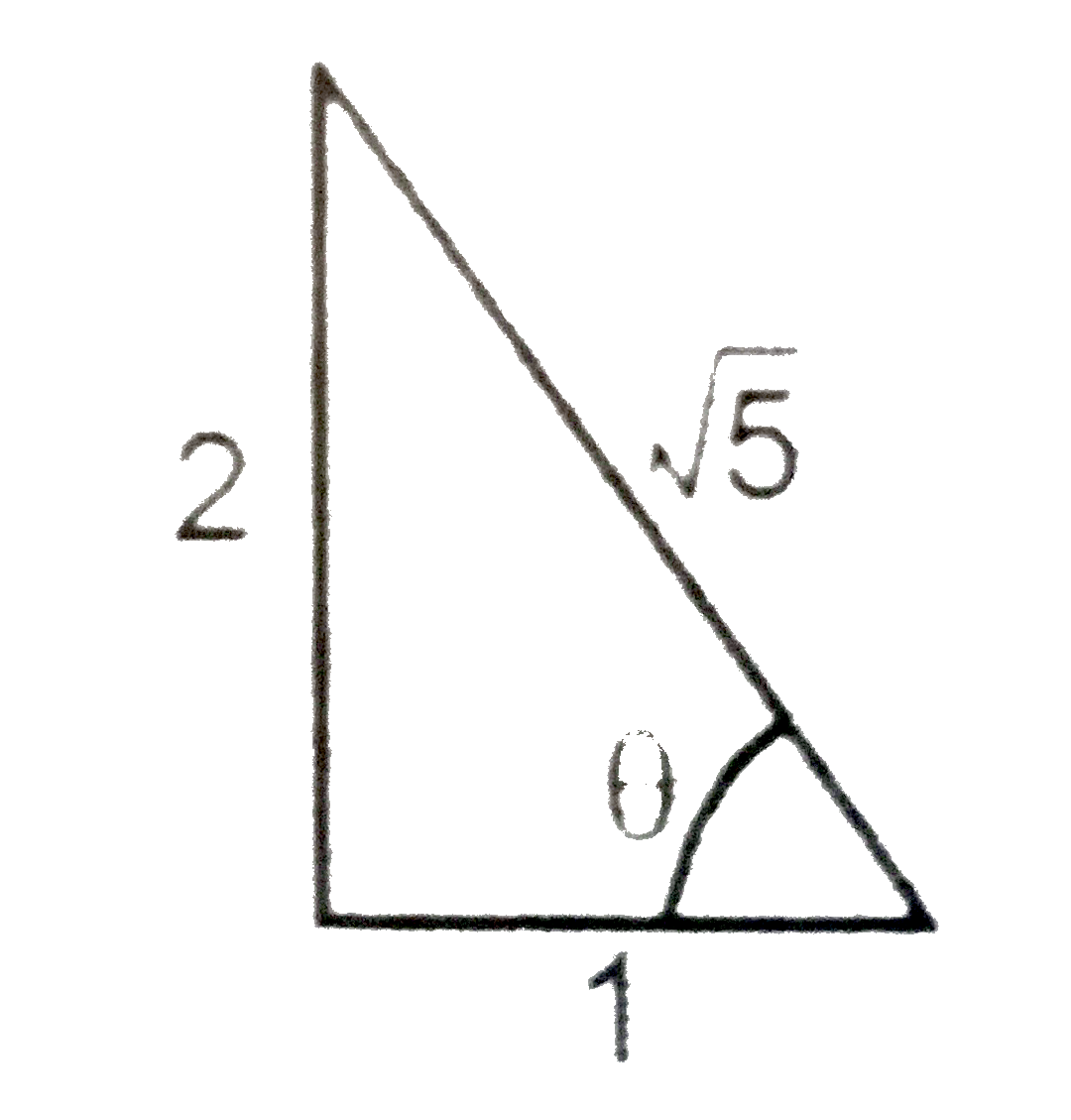
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
41 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Knowledge Check
A particle is projected with a velocity v, so that its range on a horizontal plane is twice the greatest height attained. If g is acceleration due to gravity, then its range is :
A4v25gB4g5v2C4v35g2D4v5g2A particle is projected with a velocity v such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is (where g is acceleration due to gravity)
A4v25gB4g5v2Cv2gD4v2√5gIf R is the maximum horizontal range of a particle, then the greatest height attained by it is :
ARB2RCR/2DR/4
A body is projected with velocity u so that its horizontal range is twice the maximum height.The range is
View SolutionA particle is projected with speed v=√150m/s from the horizontal surface such that its range on the horizontal plane is twice the greatest height attained by it. Then half of range of the projectile in meter is (use g = 10 m/s2)
View SolutionA particle is projected so as to have a range R on a horizontal plane through the point of projection and the greatest height attained by it is h. The maximum horizontal range with this velocity of projection is
2h+R28h or u={2g(h+R216h)}1/2
View SolutionA particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is
View Solution
