When a particle is thrown horizontally, the resultant velocity of the projectile at any time t is given by:-
gt
12gt2
√u2+g2t2
√u2−g2t2
The correct Answer is:C
To find the resultant velocity of a projectile when a particle is thrown horizontally, we can follow these steps:
1. Identify the Components of Velocity:
- When a particle is thrown horizontally, it has two components of velocity:
- Horizontal component (vx)
- Vertical component (vy)
2. Determine the Horizontal Component:
- The horizontal component of velocity remains constant throughout the motion since there are no horizontal forces acting on the particle (assuming air resistance is negligible).
- Let the initial horizontal velocity be u. Therefore,
vx=u
3. Determine the Vertical Component:
- The vertical component of velocity changes due to the acceleration caused by gravity.
- The initial vertical velocity is 0 (since it is thrown horizontally).
- The vertical component of velocity at time t can be calculated using the equation:
vy=uy+gt
where uy=0 (initial vertical velocity) and g is the acceleration due to gravity.
- Thus,
vy=0+gt=gt
4. Calculate the Resultant Velocity:
- The resultant velocity (v) of the projectile can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular to each other:
v=√v2x+v2y
- Substituting the values of vx and vy:
v=√u2+(gt)2
5. Final Result:
- Therefore, the resultant velocity of the projectile at any time t is given by:
v=√u2+(gt)2
- When a particle is thrown horizontally, it has two components of velocity:
- Horizontal component (vx)
- Vertical component (vy)
- The horizontal component of velocity remains constant throughout the motion since there are no horizontal forces acting on the particle (assuming air resistance is negligible).
- Let the initial horizontal velocity be u. Therefore,
vx=u
- The vertical component of velocity changes due to the acceleration caused by gravity.
- The initial vertical velocity is 0 (since it is thrown horizontally).
- The vertical component of velocity at time t can be calculated using the equation:
vy=uy+gt
where uy=0 (initial vertical velocity) and g is the acceleration due to gravity.
- Thus,
vy=0+gt=gt
- The resultant velocity (v) of the projectile can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular to each other:
v=√v2x+v2y
- Substituting the values of vx and vy:
v=√u2+(gt)2
- Therefore, the resultant velocity of the projectile at any time t is given by:
v=√u2+(gt)2
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
41 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
When a particle is thrown horizontally from certain height above the ground with an initial velocity u, the speed of the particle at any time t before striking the ground is given by
(A) gt
(B) 12gt2
(C) √u2+g2t2
(D) √u2−g2t2
View SolutionIf a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View Solution
Knowledge Check
For a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?A−9ms−1B−12ms−1C3ms−1D42ms−1A projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
Av0sinα vertically downwardB2v0sinα vertically downwardC2v0sinα vertically upwardDzeroA javelin thrown into air at an angle with the horizontal has a range of 200 m. If the time of flight is 5 second, then the horizontal component of velocity of the projectile at the highest point of the trajectory is
A40m/sB20m/sC9.8m/sD5m/s
A particle is thrown with velocity u at an angle ∝ from the horizontal. Another particle is thrown with the same velocity at an angle ∝ from the verticle. What will be the ratio of times of flight of two particles ?
View SolutionAcceleration of a particle is given by
a=1/V
Where V is the velocity . Find
(i) Velocity of particle at time t, given that v = 10 m/s at t = 0.
(ii) Velocity of particle when its position is x, given that speed is 3 m/s at x = 0.
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View SolutionThe coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
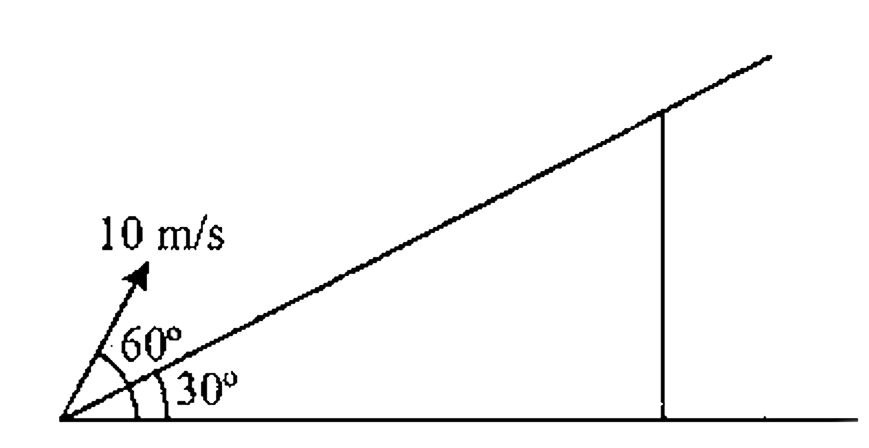
View Solution