Assertion: When a particle moves with constant velocity its average velocity, its insttantaneous velocity and its speed are all equal in magnitude.
Reason: If the average velocity of a particle moving on a straight line is zero in a time interval, then it is possible that the instantaneous velocity is never zero in the internal.
If both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.
If both Assertion & Reason are True but Reason is not correct explanation of the Assertion.
If Assertion is Trie but the Reason is False.
If both Assertion & Reason are false
The correct Answer is:C
To analyze the assertion and reason provided in the question, let's break it down step by step.
Step 1: Understanding the Assertion
The assertion states that when a particle moves with constant velocity, its average velocity, instantaneous velocity, and speed are all equal in magnitude.
- Constant Velocity: This means that both the speed (magnitude of velocity) and direction of the particle do not change over time.
- Average Velocity: This is defined as the total displacement divided by the total time taken. For constant velocity, the displacement is linear, and thus the average velocity remains constant and equal to the instantaneous velocity.
- Instantaneous Velocity: This is the velocity of the particle at a specific moment in time. Since the particle is moving with constant velocity, the instantaneous velocity at any point in time is the same as the average velocity.
- Speed: This is the magnitude of the velocity vector. Since the velocity is constant, the speed remains constant as well.
Conclusion for Assertion: The assertion is true because all three quantities (average velocity, instantaneous velocity, and speed) are equal in magnitude when the particle moves with constant velocity.
Step 2: Understanding the Reason
The reason states that if the average velocity of a particle moving in a straight line is zero over a time interval, then it is possible that the instantaneous velocity is never zero during that interval.
- Average Velocity Zero: This occurs when the displacement of the particle is zero over the time interval, meaning the particle starts and ends at the same position.
- Instantaneous Velocity: This can be non-zero even if the average velocity is zero. For example, a particle could move away from the starting point and then return to it, having a non-zero instantaneous velocity at various points during its motion.
Conclusion for Reason: The reason is true because it is possible for a particle to have non-zero instantaneous velocities throughout its motion while still having an average velocity of zero.
Final Conclusion
- The assertion is true.
- The reason is also true.
The assertion states that when a particle moves with constant velocity, its average velocity, instantaneous velocity, and speed are all equal in magnitude.
- Average Velocity: This is defined as the total displacement divided by the total time taken. For constant velocity, the displacement is linear, and thus the average velocity remains constant and equal to the instantaneous velocity.
- Instantaneous Velocity: This is the velocity of the particle at a specific moment in time. Since the particle is moving with constant velocity, the instantaneous velocity at any point in time is the same as the average velocity.
- Speed: This is the magnitude of the velocity vector. Since the velocity is constant, the speed remains constant as well.
The reason states that if the average velocity of a particle moving in a straight line is zero over a time interval, then it is possible that the instantaneous velocity is never zero during that interval.
- Instantaneous Velocity: This can be non-zero even if the average velocity is zero. For example, a particle could move away from the starting point and then return to it, having a non-zero instantaneous velocity at various points during its motion.
- The assertion is true.
- The reason is also true.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
When a particle moves with constant velocity, its average velocity, its instantaneous velocityi and its speed are all equal. Comment on this statement.
View SolutionWhen a particle moves with constant velocity its average velocity, its instantaneous velocity and its speed all are equal. Is this statement true or false ?
View Solution
Knowledge Check
If average velocity of particle moving on a straight line is zero in a time interval, then
AAcceleration of particle may be zeroBVelocity of particle must be zero at an instantCVelocity of particle may be never zero in the intervalDAverage speed of particle may be zero in the intervalFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
A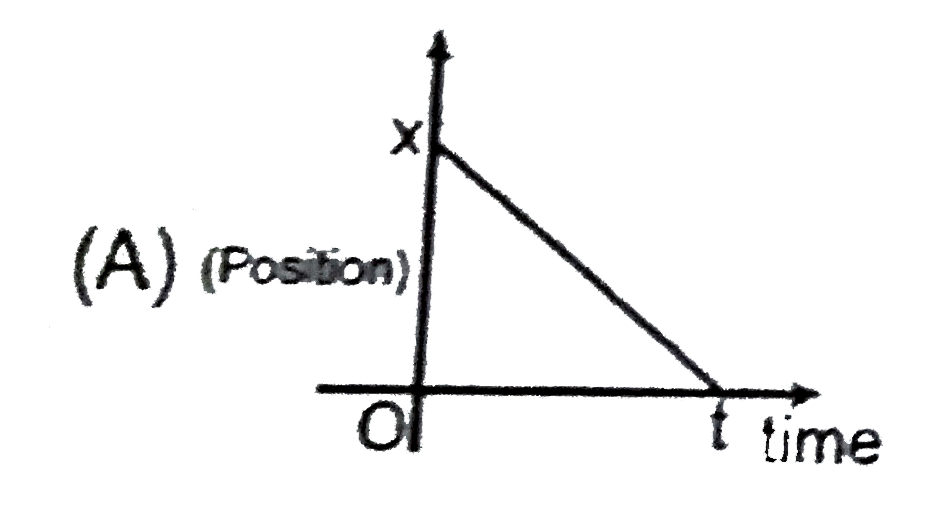 B
B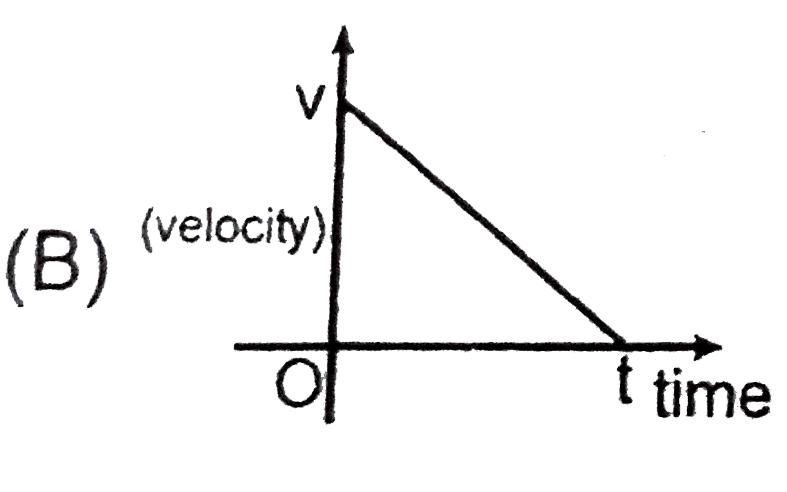 C
C D
D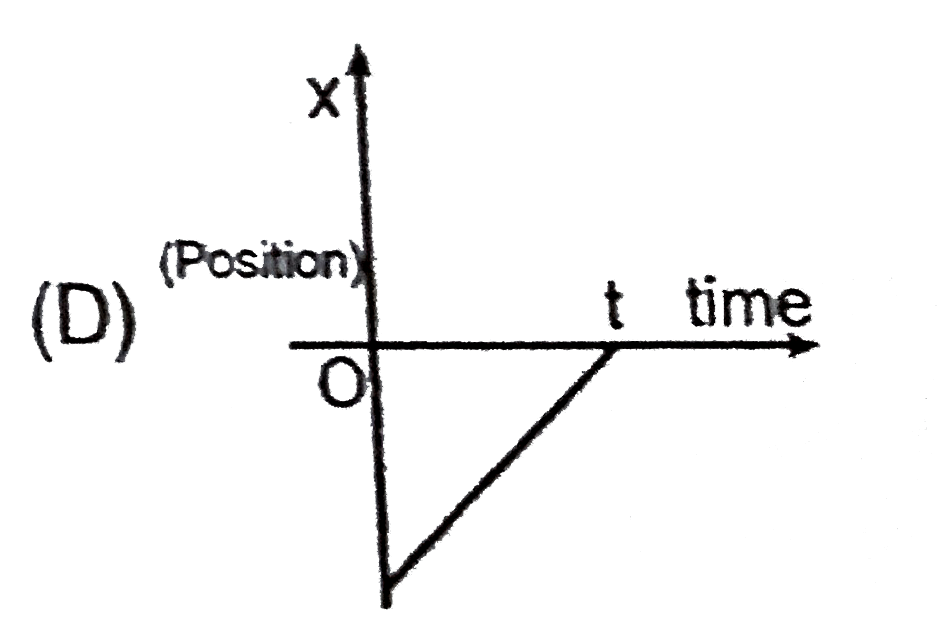
Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
Au+12atBu+atCu+at2Du2
A car moves with a contant velocity m its average velocity is equal to its______
View SolutionA car moves with a contant velocity m its average velocity is equal to its______
View SolutionIf a particle is moving with a constant velocity, what is its acceleration?
View SolutionThe average velocity of a particles is equal to its displacement-time graph ?
View SolutionThe average velocity of a particle moving on a straight line is zero in a time interval.
Assertion :− It is possible that the instantaneous acceleration is never zero in the interval.
Reason :− It is possible that the instantaneous velocity is never zero in the interval.
View Solution
