A body A is thrown up vertically from the ground with velocity V0 and another body B is simultaneously dropped from a height H. They meet simultaneously dropped from a height H. They meet at a height H2 if V0 is equal to
√2gH
√gH
12√gH
√2gH
The correct Answer is:B
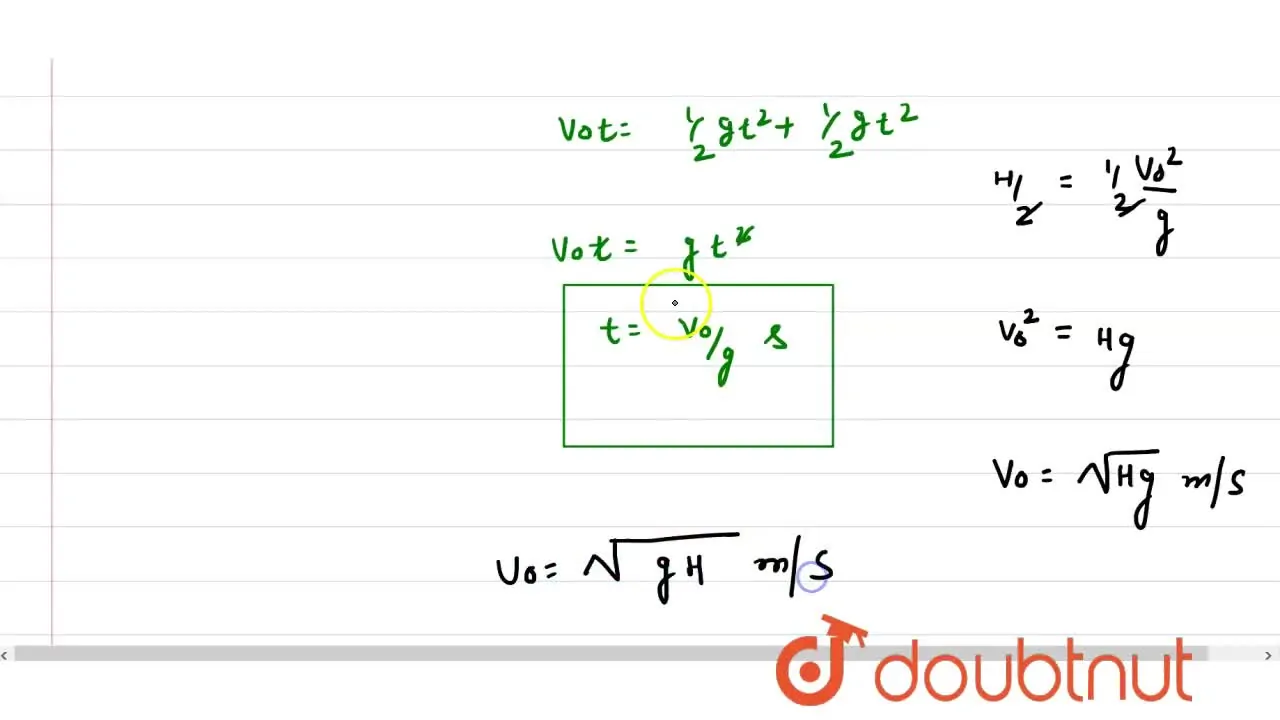
fLet the two bodies A and B respectively meet at a time, at a height H2 from the ground.

Using S=ut+12at2
For a body A,u=V0,a=−g,S=H2
∴H2=v0t−12gt2..............(i)
For a body B,u=0,a=+g/g,S=H2
∴H2=12gt2 ..........(ii)
Equating equation (i) and (ii) we get
V0t−12gt2=12gt2
V0t=gt2 or t=V0g
Substituting the value of t is equation (i), we get
H2=V0×(V0g)−12g(V0g)2=V20V0−12V20g
H2=12V20g or v20=gH
V0=√gH
Related Playlists
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2170videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-341videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
A body is dropped from a certain height.
View SolutionA body is dropped vertically from a certain height. Draw velocity time graph of the body.
View SolutionA body A is thrown vertically upwards with initial velocity v1. Another body B is dropped from a height h. Find how the distance x between the bodies depends on the time t if the bodies begin to move simultaneously.
View SolutionA body is just dropped from a height. What is its initial velocity?
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA body is projected vertically up from ground with a velocity u so as to reach maximum height 'h'. At half of the maximum height its velocity will be
View SolutionA body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
View SolutionOne body is thrown up with velocity of 34.6ms 1. Another body is dropped from a height of 50m. Relative acceleration between the two bodies is
View SolutionA body A is thrown vertically upwards with such a velocity that it reaches a maximum height of h. Simultaneously, another body B is dropped from height h. It strikes the ground and does not rebound. The velocity of A relative to B versus time graph is best represented by (upward direction is positive).
View SolutionA ball is thrown vertically upward with speed 40m/s. Simultaneously, another ball is dropped from a height 200m in the same verticle line. When and where the balls meet?
View Solution