Which of the following equation represents the motion of a body moving with constant finite acceleration ? In these equation, y denotes the displacement in time t and p.q and r the arbitary constants ?
y=(p+qt)(r+pt)
y=p+tqr
y=(p+t)(q+t)(r+1)
y=(p+qt)r
The correct Answer is:C
To determine which of the given equations represents the motion of a body moving with constant finite acceleration, we need to analyze each equation. We will differentiate the equations to find the acceleration and check if it is constant and finite.
1. Understanding the Problem: We need to find which equation represents motion with constant finite acceleration. The acceleration can be determined by taking the second derivative of the displacement y with respect to time t.
2. Analyzing the First Option:
- Equation: y=p+qt+rt2
- Differentiate once to find velocity:
dydt=q+2rt
- Differentiate again to find acceleration:
d2ydt2=2r
- Since r is a constant, the acceleration is constant and finite.
3. Analyzing the Second Option:
- Equation: y=p+qt
- Differentiate once:
dydt=q
- Differentiate again:
d2ydt2=0
- The acceleration is zero, which is not finite acceleration.
4. Analyzing the Third Option:
- Equation: y=p+qt+rt
- Differentiate once:
dydt=q+r
- Differentiate again:
d2ydt2=0
- The acceleration is zero, which is not finite acceleration.
5. Analyzing the Fourth Option:
- Equation: y=p+qt+rt2
- Differentiate once:
dydt=q+2rt
- Differentiate again:
d2ydt2=2r
- Since r is a constant, the acceleration is constant and finite.
Conclusion:
From the analysis, the equations that represent motion with constant finite acceleration are:
- First Option: y=p+qt+rt2
- Fourth Option: y=p+qt+rt2
Final Answer:
The correct equations representing the motion of a body with constant finite acceleration are the First Option and the Fourth Option.
---
- Equation: y=p+qt+rt2
- Differentiate once to find velocity:
dydt=q+2rt
- Differentiate again to find acceleration:
d2ydt2=2r
- Since r is a constant, the acceleration is constant and finite.
- Equation: y=p+qt
- Differentiate once:
dydt=q
- Differentiate again:
d2ydt2=0
- The acceleration is zero, which is not finite acceleration.
- Equation: y=p+qt+rt
- Differentiate once:
dydt=q+r
- Differentiate again:
d2ydt2=0
- The acceleration is zero, which is not finite acceleration.
- Equation: y=p+qt+rt2
- Differentiate once:
dydt=q+2rt
- Differentiate again:
d2ydt2=2r
- Since r is a constant, the acceleration is constant and finite.
From the analysis, the equations that represent motion with constant finite acceleration are:
- First Option: y=p+qt+rt2
- Fourth Option: y=p+qt+rt2
The correct equations representing the motion of a body with constant finite acceleration are the First Option and the Fourth Option.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
41 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Knowledge Check
Which of the following represents the motion of a body moving in a straight line under constant acceleration ?
A B
B C
C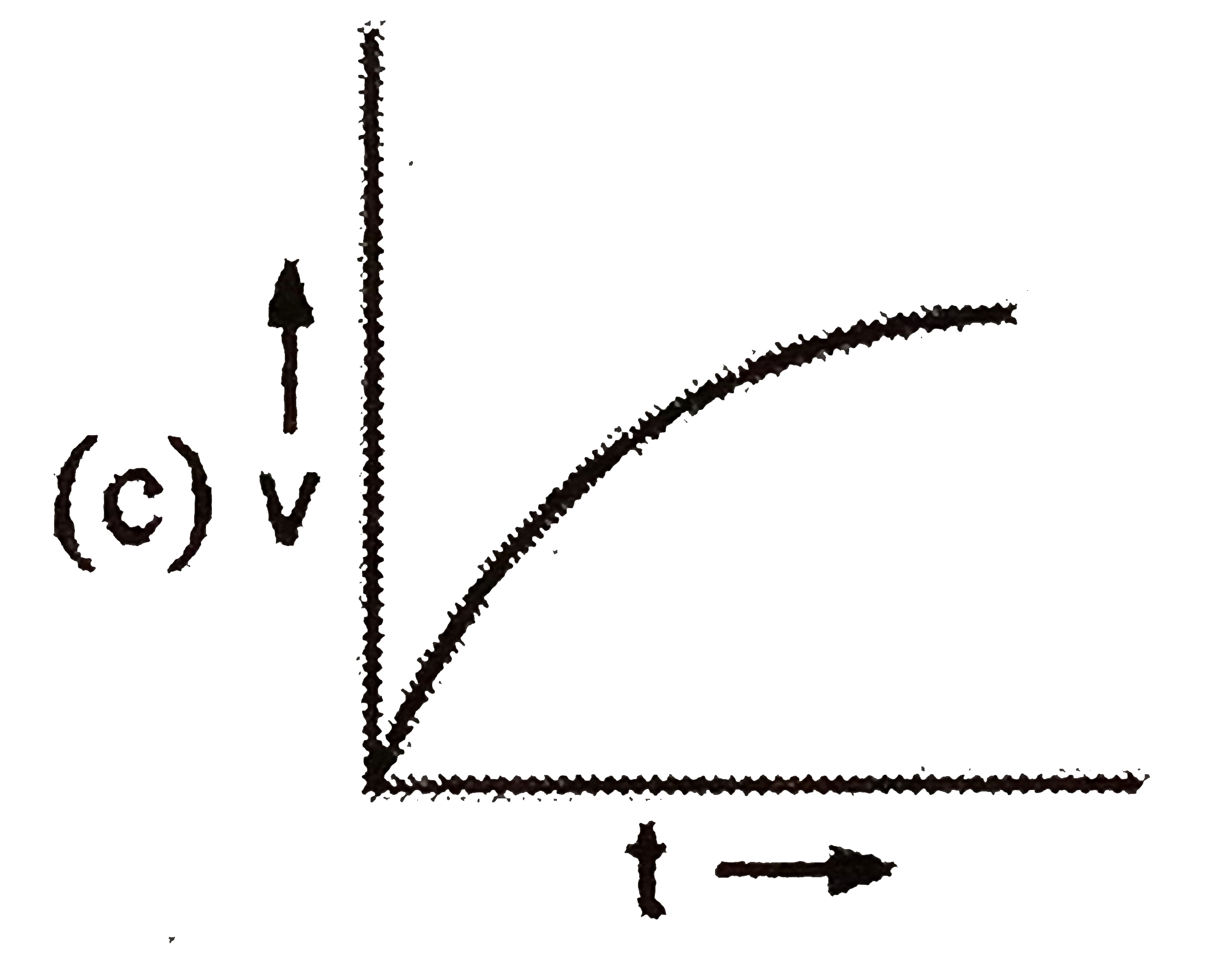 D
D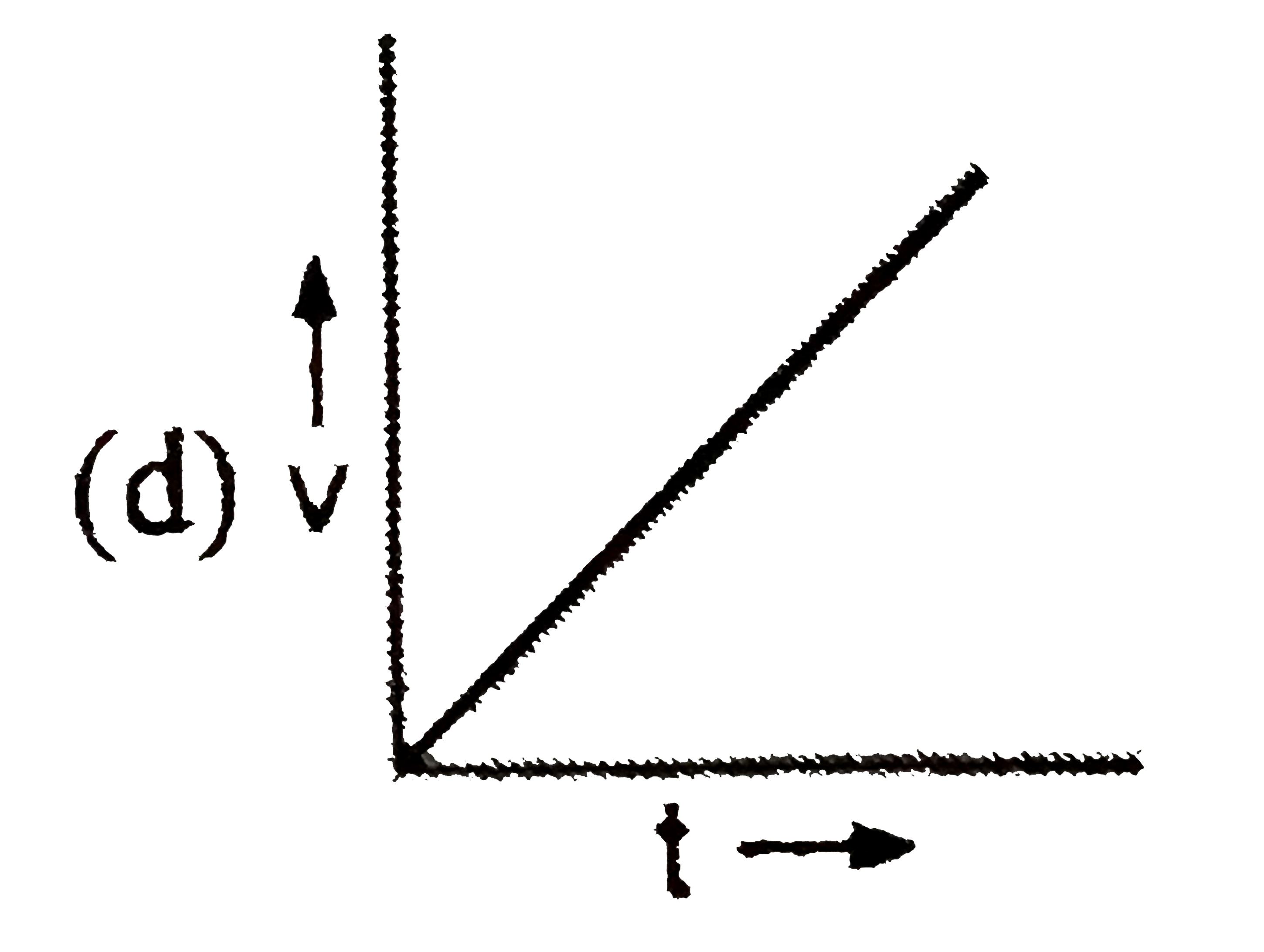
Which of the following relations representing displacement x (t) of particle describes motion with constant acceleration?
Ax=6-7 t−2Bx=3t2+5t3+7Cx=9t2+8Dx=4t−23t−1Which of the following represents a stationary wave ? (a, b, c are constants in the equation)
Ay=acos(2bx)sin(ct)By=asin(cx)sin(2bt)Cy=acos(bx+ct)Dy=asin(bx−ct)
What is the nature of the displacement time curve of a body moving with constant acceleration ?
View SolutionWrite down the three equations of motion for a particle moving with constant acceleration.
View SolutionDerive the following equations of motion for an object moving with constant acceleration along a straight line : snth=v0+a2(2n−1).
View SolutionWhat is the nature of the displacement-time curve of a body moving with constant velocity ?
View Solutionwhich of the following function corrtly represent the traveling wave equation for finite values of x and t ?
View Solution