In R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
2α+β+2γ+2=0
2α−β+2γ+4=0
2α+β−2γ−10=0
`2alpha- beta+ 2gamma-8=0`
The correct Answer is:b, d
Clearly, plane P3 is P2+λP1=0.
⇒ x+λy+z−1=0
Distance of this plane from point (0,1,0) is 1.
⇒ 0+λ+0−1√1+λ2+1=±1
∴ λ=−12
Thus, equation of P3 is 2x−y+2z−2=0.
Distance of this plane from point (α,β,γ) is 2.
⇒ ∣∣∣2α−β+2γ−23∣∣∣=2
⇒ 2α−β+2γ=2±6
Thus, option (b), (d) are correct.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Numerical)10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank34videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
In R', consider the planes P1,y=0 and P2:x+z=1. Let P3, be a plane, different from P1, and P2, which passes through the intersection of P1, and P2. If the distance of the point (0,1,0) from P3, is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation is (are) true ?
View SolutionIn R', consider the planes P1,y=0 and P2:x+z=1. Let P3, be a plane, different from P1, and P2, which passes through the intersection of P1, and _2P If the distance of the point (0,1,0) from P3, is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation is (are) true ?
View Solution
Knowledge Check
- Question 1 - Select One
P1:x+3y−z=0andP2,y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
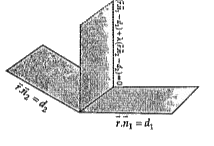
Equation of P3 isA4x + y - 2z = 10Bx + y - 2z = 3Cx + 9y + 11z = 0D4x - y + z = 0 - Question 2 - Select One
A plane P passes through the line of intersection of the planes 2x−y+3z=2,x+y−z=1 and the point (1,0,1).
What is the equation of the plane P?A2x+5y−2=0B5x+2y−5=0Cx+z−2=0D2x−y−2z=0 - Question 3 - Select One
P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
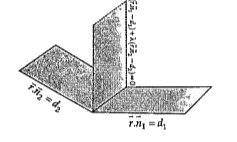
__________ is a point on P3.A(1,2,3)B(-1,4,3)C(-6,-3,3)D(6,3,-3)
A plane P passes through the line of intersection of the planes 2x−y+3z=2.x+y−z=1 and the point (1,0,1)
What is the equation of the plane P?View SolutionLet two planes p1:2x−y+z=2andp2:x+2y−z=3 are given :
equation of the plane through the intersection of p1andp2 and the point (3,2,1) is :View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
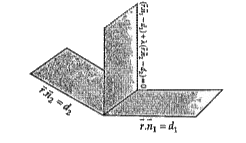
Distance of P3 from origin is _______ units.View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2

The angle between P1andP2 is ________.View SolutionLet P1:x−2y+3z=5andP2:2x−3y+z+4=0 be two planes. The equation of the plane perpendicular to the line of intersection to the line of intersection of P1=0 and P2= and passing through (1,1,1) is
View Solution

