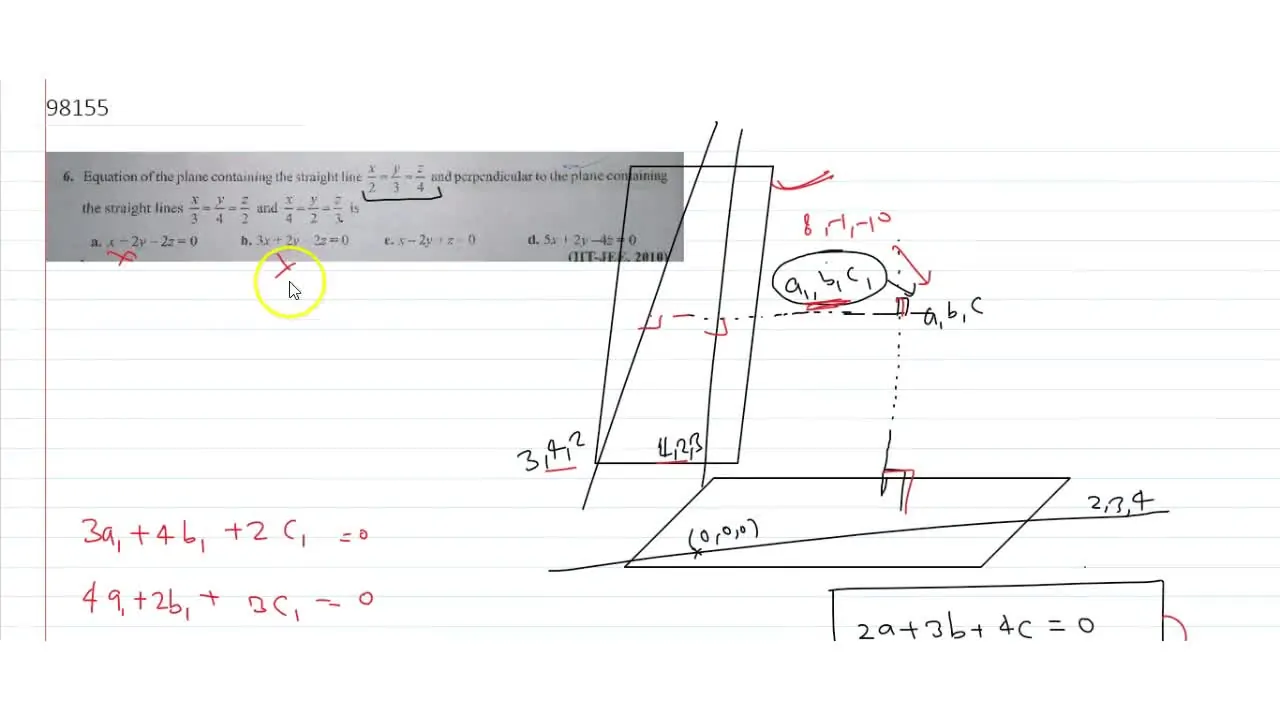
Equation of the plane containing the straight line x2=y3=z4 and perpendicular to the plane containing the straight lines x2=y4=z2 and x4=y2=z3 is
x+2y−2z=0
3x+2y−2z=0
x−2y+z=0
5x+2y−4z=0
The correct Answer is:c
Plane 1:ax+by+cz=0 contains line x2=y3=z4
∴ 2a+3b+4c=0
Plane 2:a'x+b'y+c'z=0 is perpendicular to plane containing lines x3=y4=z2andx4=y2=z3
∴ 3a'+4b'+2c'=0and4a'+2b'+3c'=0
⇒ a'12−4=b'8−9=c'6−16
⇒ 8a−b−10c=0 (ii)
From (i) and (ii),
a−30+4=b32+20=c−2−24
⇒ Equation of plane x−2y+z=0
Related Playlists
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Numerical)10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank34videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
The equation of the plane containing the straight line x2=y3=z4 and perpendicular to the plane containing the straight lines x3=y4=z2andx4=y2=z3 is :
View SolutionEquation of the plane containing the straight line x2=y3=x4 and perpendicular to the plane containing the straight lines x3=y4=x2 is
View SolutionThe equation of the plane containing the straight line x2=y3=z4 and perpendicular to the plane containing the straight lines x3=y4=z2andx4=y2=z3 is
px+qy+r=0, then p+q+r isView SolutionEquation of the plane containing the straighat line x2=y3=z4 and perpendicular to the lane containing the straighat lines x3=y4=z2andx4=y2=z3 is (A) x+2y−2z=0 (B) 3x+2y−2z=0 (C) x−2y+z=0 (D) 5x+2y−4z=0
View SolutionThe equation of the plane containing the straight line x2=y3=z4 and perpendicular to the plane containing the straight lines x3=y4=z2andx4=y2=z3 is :
View SolutionFind the equation of the plane containing the straight line x−12=y+2−3=z5 and perpendicular to the plane x−y+z+2=0.
View SolutionThe equation of the plane containing the lines x−12=y+1−1=z3 and x2y−2−1=z+13 is
View SolutionFind the equation of the plane passing through the straight line x−12=y+2−3=z5 and perpendicular to the plane x−y+z+2=0.
View SolutionFind the equation of plane containing the line x−24=y−13=z+1−2 aond perpendicular to the plane 2x−y+2z=11.
View SolutionThe equation of the plane containing the line 2x−5y+z=3,x+y+4z=5 and parallel to the plane x+3y+6z=1, is
View Solution