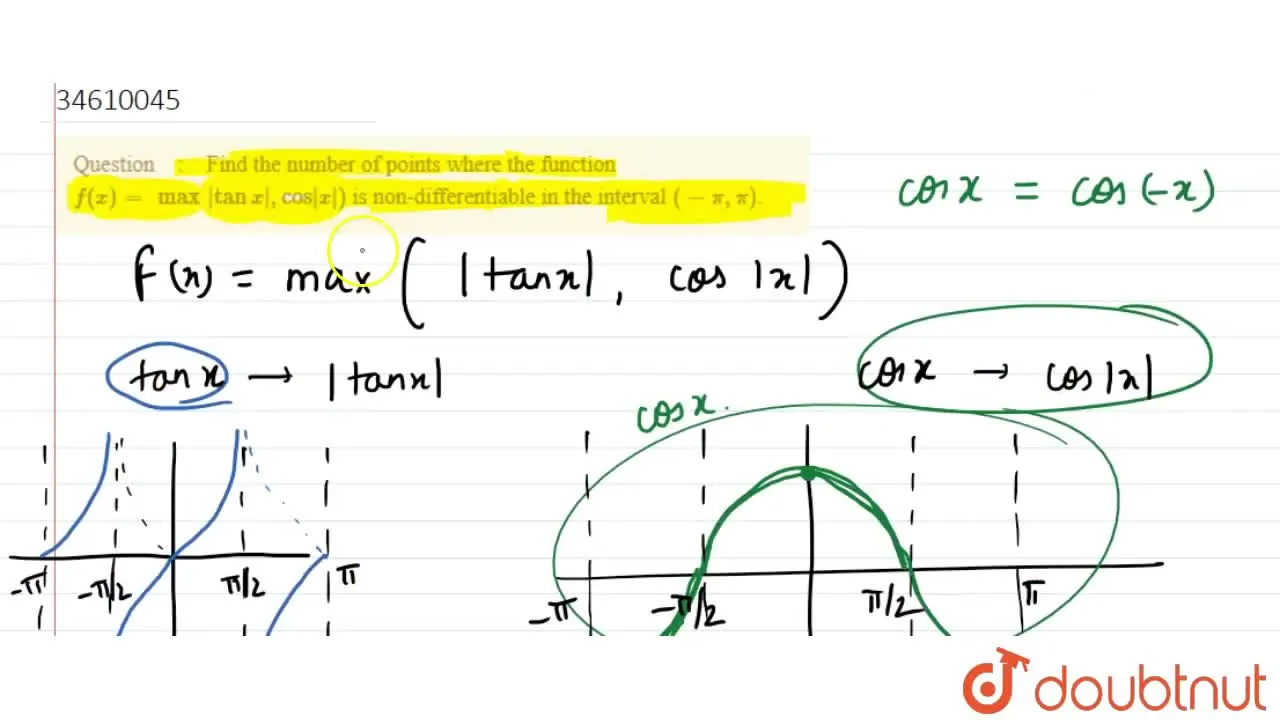
Find the number of points where the function f(x)=max|tanx|,cos|x|) is non-differentiable in the interval (−π,π).
Step by step video & image solution for Find the number of points where the function f(x)=max|tanx|,cos|x|) is non-differentiable in the interval (-pi,pi). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Similar Questions
Number of points where f(x)=max{2−|x|,min{x2−1}} is not differentiable.is
View SolutionFind the number of critical points of the function
f (x) = min (tan x , cos x) , x∈(0,π)View SolutionNumber of points where f(x)=|x-sgn(x)| is non differentiable is (sgn( ) denotes signum function )
View SolutionIn (0,2π), the total number of points where f(x)=max.{sin x, cos x, 1 - cos x} is not differentiable , are equal to
View SolutionThe number of points of non - differentiabil ity for the function f(x)=|x|+|cosx|+tan(x+π4) in the interval (−1,2) is
View Solutionlet S be the set of all points in (−π,π) at which the function , f(x) =min {sinx , cos x} is not differentiable Then S is a subset of which of the following ?
View SolutionThe number of points where f(x) = max {|sin x| , | cos x|} , x∈(−2π,2π) is not differentiable is ______
View SolutionIf f(x)=∣∣x2−3x+2∣∣+|sinx| then number of points where f(x) is not differentiable in [−π,π] is
View SolutionVerify Rolle's Theorem for the functions :
f(x)=tanx, defined in the interval [0,π].View Solutionf:(0,∞)⇒R f(x)=max(x2,|x|) then the number of points where function is non- differentiable,is
View Solution